One argument used to rationally support the existence of God is the ontological argument. There are many forms of ontological arguments, but I’ll only use a few different versions here, each one mainly derived from Anselm’s approach. The ontological argument for the existence of God was first structured in the Proslogion of Saint Anselm, Archbishop of Canterbury (1033-1109 A.D.); though it was actually Immanuel Kant, an 18th century German philosopher, who first called the argument “ontological.” Ontology is a branch of metaphysics concerned with the nature and relations of being. Ontology attempts to answer such questions like, “What is real?” Thus Anselm’s ontological proof attempts to answer the question of whether or not God is real. “What’s metaphysics?” you may ask. Metaphysics is itself a branch of philosophy that studies the nature and causes of things. Metaphysics asks questions like, “Does matter exist?” and “Does the immaterial (e.g. the soul) exist?”
Besides Anselm, Descartes, Leibniz, Spinoza, Hegel and Godel also made notable versions of the ontological argument. Some believe that the type of argument used by Anselm and others should be called a “modal” argument because of its reliance on the modal concepts of possibility, actuality, and necessity (I’ll explain what those words mean a little later). Both of the premises I’ll use in this article come from Anselm’s ontological argument and use symbolic logic to arrive at the conclusion. If you’re concerned about encountering difficulty in understanding this symbolic logic stuff you needn’t worry. Understanding the symbols is actually quite easy and won’t take long to explain.
Anselm defines God by saying God is that “which nothing greater can be conceived.” One way to interpret this phrase is to define “God” as maximal perfection, i.e. the greatest possible being (and this is the definition that the ontological argument will use here). Some may criticize this definition by saying that’s not what they mean when they use the term God. But that really doesn’t matter. If the argument proves that such a being exists, then it does so regardless of what one wishes to call the being of maximal perfection. Furthermore, it’s unclear why a rational person should be reluctant to call such a being God, or why God wouldn’t be the greatest possible being.
Defining God as “the greatest possible being” has a number of interesting consequences. One of them is that it becomes significantly more difficult, if not impossible, to demonstrate that God is not possible. For instance, God is said to have perfect power: omnipotence. But can God create a round square? Can he defy such basic rules of logic? The theist under this definition of God could reply that God is only omnipotent to the greatest possible extent. Thus, this theist could respond by claiming that God cannot do what is logically impossible, but He can do anything that can be done. If a certain level of one of God’s traditional qualities is proved “impossible,” this theist could then lower the bar on that aspect of God down to where that quality is possible, such as from, “God is omnipotent and can do literally anything,” to “God is omnipotent to the greatest possible extent.”
There are a number of ways to describe the ontological argument. One way to do so is through reductio ad absurdum (“reduction to absurdity”). In a reductio ad absurdum argument, the negation (opposite) of the conclusion is assumed, and then demonstrated that the opposite of this conclusion leads to an absurdity (such as a contradiction). Incidentally, Anselm himself used a reductio ad absurdum argument in the book Proslogion to explain his ontological argument.
If therefore that than which nothing greater can be conceived exists in the understanding alone [and not in reality], then this thing than which nothing greater can be conceived is something than that which a greater can be conceived. And this is clearly impossible. Therefore, there can be no doubt at all that something than which a greater cannot be conceived exists in both the understanding and in reality.
To explain this sort of thing more clearly, I’ve written a similar version of this argument (which has paraphrased significant amounts of what Anselm wrote):
Conclusion: Statement 7 is absurd. It can’t possibly be true because it is self-contradictory. Therefore, God must exist in reality as well as the mind.
You might be wondering about the objections to the ontological argument. Well, stay tuned, because I’ll get to that later after I describe the symbolic logic approach. Some of the objections that we’ll see apply more clearly to the symbolic logic method than the reductio ad absurdum one. Of course, if the argument is wrong, there must be a reason why it is wrong. There are essentially two ways a deductive argument like this one can fail. One is that at least one of the premises is incorrect. In that case, the question would be “which premise fails and why?” The other way is that the argument is invalid, i.e. the argument does not logically follow somewhere along the way. If that is true, which line of the argument does not logically follow from the statement(s) it’s based upon? The same questions apply to the symbolic logic approach, except that the symbolic logic argument actually eliminates invalidity as a possibility (more later).
Before I further explain the symbolic logic approach, it’s best one know about a division of logic that I’ll be using called modal logic. If you think you know enough about symbolic logic (including modal logic) to see the argument for yourself right away, click here. If not, read on.
To help explain some basic concepts of modal logic, let me tell you a little story about OmniSim. Our world is reality. Nevertheless, there are many other ways reality could have been like, i.e. many other possible worlds. Suppose we have a supercomputer called OmniSim that can simulate all possible worlds. Every world that is possible has a simulated environment in this supercomputer. (I’ll refer to this hypothetical supercomputer a little later when I describe a few terms.) Modal logic mainly deals with “necessary” (signified by a square, like this one: ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ) and “possible” (signified by a diamond, like this one:
) and “possible” (signified by a diamond, like this one:  ) modal operators. For example:
) modal operators. For example:
 p
p
This means that p is possibly true. According to  p, there exists at least one possible world in OmniSim where p is true. An example of a possible (but not necessary) statement would be that Abraham Lincoln was not president of the United States. This is indeed possible, but not necessary. There exists a world in OmniSim (even if it is not our own) where Abraham Lincoln was never such a President, because such a world is possible. However, there also exists at least one possible world where Abraham Lincoln was in fact the President of the U.S. (e.g. our own). Therefore, the statement is possible even if it is not true in every possible world. A statement that’s true in some possible worlds but also false in some other possible worlds is called a contingent statement (because it can be either true or false). Another example:
p, there exists at least one possible world in OmniSim where p is true. An example of a possible (but not necessary) statement would be that Abraham Lincoln was not president of the United States. This is indeed possible, but not necessary. There exists a world in OmniSim (even if it is not our own) where Abraham Lincoln was never such a President, because such a world is possible. However, there also exists at least one possible world where Abraham Lincoln was in fact the President of the U.S. (e.g. our own). Therefore, the statement is possible even if it is not true in every possible world. A statement that’s true in some possible worlds but also false in some other possible worlds is called a contingent statement (because it can be either true or false). Another example:
![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) p
p
This means that p is necessarily true. That is, it is true in all possible worlds. Using the supercomputer analogy, statement p would be true in all of OmniSim’s simulated worlds. Examples of a necessary truth would be 2 + 2 = 4, the law of noncontradiction (this law states that for any specified proposition p, it is impossible for both p and not p to be true; e.g. it is impossible for me to exist and to not exist at the same time), and the law of excluded middle (which I describe a little later). All of these things are true in all possible worlds. Note that a possible statement (one that’s true in at least one possible world) can also be necessary (true in all possible worlds), and all necessary statements are possible. However, a contingent statement (one that’s true in some possible worlds, and false in some others) cannot be a necessary statement, and no necessary statements are contingent. A brief summary of the terms that describe statements can be found below. All three of those terms belong to the category of modal status, because they describe statements as being necessarily true/false, possibly true/false, or contingently true/false. The table after those definitions is a summary of the basic modal symbolic stuff we’ve got so far.
| Term | Meaning |
|---|---|
| possible | True in at least one possible world. |
| contingent | True in some possible worlds, false in some possible worlds. |
| necessary | True in all possible worlds. |
| Symbolic Logic | What it means |
|---|---|
| p | p is true in actuality (i.e. p is true in the real world). |
 p p
| p is possibly true (i.e. p is true in at least some possible worlds). |
![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) p p | p is necessarily true (i.e. p is true in at all possible worlds). |
One reason to use symbolic logic is that this can actually provide us with a formal proof. To be fair, a formal proof in symbolic logic can only demonstrate the argument to be valid. In logic, valid just means that, if all the premises are true, then the conclusion must be true also. A valid argument isn’t necessarily sound. A sound argument is an argument that is both valid and has all its premises being true. An invalid argument is where one can have all true premises and yet still have a false conclusion. Why use symbolic logic? As already mentioned, an argument can actually be proved valid. When an argument is proved valid, one cannot rationally claim that it is invalid as a way to doubt the soundness of the argument. Instead, the only reasonable way left to attack the argument is to attack its premises. Another reason to use symbolic logic is that it uses single letters to represent entire statements. Such letters are called statement (or propositional) constants. Statement constants provide an easy way to avoid writing out a lot of English, and make it easier (sometimes a lot easier) to focus on the logical structure of the argument at hand, whereas explaining some premises in words can get a little messy. A premise in symbolic logic (using single letters to represent statements) can be much more concise and much easier to understand, especially with very large and compounded statements. The reductio ad absurdum argument described above is neat enough to easily and clearly explain in words, but that is not quite the case with this formal proof.
In essence, the formal proof for the ontological argument shows this:
Conclusion: God exists in reality. |
Incredible as it may seem, it can be done. And that’s what the proof demonstrates. The only thing left then is to attack the premises. Looking back on it, the validity of the argument may not be so incomprehensible. In the reductio ad absurdum argument, for example, only the first three premises need to be true. The conclusion rolls right out after that (as explained by the later statements in the argument). Before moving on with the symbols, let’s first look at the justification that has been used to justify those first two premises:
I put the if in bold to demonstrate that the first premise doesn’t presuppose the existence of God, because the claim of God having necessary existence only holds if He exists (at least in this premise). Another premise that’s mentioned in the formal proof:
There are two other premises. One is the law of excluded middle and the other is called Becker’s postulate. I’ll explain what Becker’s postulate is later in this article (after I explain the other symbols used in symbolic logic) but I’ll explain the law of excluded middle right away. This logical precept states that for any proposition p, either p is true or not p is true. There is no middle ground. For example, either God exists or He does not exist.
When using statement constants that are structured in premises, it is usually meant that they are actually true in their structure. For example, if a premise just says, “p,” that premise simply means, “p is actually true.” The phrase, “If p, then q,” means, “If p is true, then q is true also.” Similarly, “Not p” means, “p is not true.”
The rest of the “need-to-know” stuff deal with the basics of symbolic logic. Once again, if you think you know enough about symbolic logic to see the argument for yourself right away, click here. If not, read on. A couple easy-to-understand and often used concepts are “negation” and “therefore.” I’ll symbolize negation using the tilde: ~.
Not pWhich means “p is not true” and is written as:
~p
“~p” is usually just read as “not p” instead of “p is not true.” The word “therefore” is symbolized with three triangular dots that look like this: 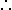 To sum it all up:
To sum it all up:
| In English | In Symbolic Logic |
|---|---|
| Not p | ~p |
| Therefore, p | 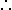 p p |
The next symbol I’ll introduce is the horseshoe:  , which signifies a conditional statement. For example,
, which signifies a conditional statement. For example,
| In English | In Symbolic Logic |
|---|---|
| If p then q | p  q q |
Using the conditional statement, some rules of inference (called inferential forms) can be gathered. One well-known one (in logic anyway) is called modus ponens. Here’s what it is:
| In English | In Symbolic Logic |
|---|---|
| If p then q p —————— Therefore, q |
p  q qp —————— 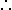 q q
|
Another rule is modus tollens and it goes like this:
| In English | In Symbolic Logic |
|---|---|
|
If p then q Not q —————— Therefore, not p |
p  q q~q —————— 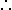 ~p ~p
|
Another symbol I’ll be using is called the wedge (also sometimes called “vee”) and it looks like 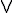 . This signifies “or.” The logical “or” is sometimes called the disjunction.
. This signifies “or.” The logical “or” is sometimes called the disjunction.
| In English | In Symbolic Logic |
|---|---|
| p or q | p 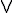 q q |
The above says that at least one of the statements (p or q) is true. Thus, even if both p and q are true, p 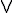 q is true. It can only be false if both p and q are false. As long as at least one of them is true, then “p
q is true. It can only be false if both p and q are false. As long as at least one of them is true, then “p 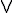 q” is true. One rule of logic I’ll be using is called disjunctive syllogism:
q” is true. One rule of logic I’ll be using is called disjunctive syllogism:
| In English | In Symbolic Logic |
|---|---|
| p or q Not p ————— Therefore, q |
p 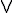 q q~p ————— 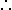 q q |
| p or q Not q ————— Therefore, p |
p 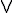 q q~q ————— 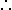 p p |
Both of the above are disjunctive syllogisms.
Now that you know the symbols, you’ll be able to more easily understand Becker’s postulate, which holds that modal status (except for actuality) is always necessary. A couple of notable examples of what this postulate implies are these two iteration axioms, so named because of the repetition of modal operators (note: there are more than two iteration axioms and more than two applications of Becker’s postulate):
| Symbolic Logic | What it Means |
|---|---|
![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) p p  ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) p p | If ![[]](https://www.angelfire.com/mn2/tisthammerw/images/bsquare.gif) p is true, then p is true, then ![[]](https://www.angelfire.com/mn2/tisthammerw/images/bsquare.gif) p is true in all possible worlds. p is true in all possible worlds. |
 p p  ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif)  p p | If  p is true, then p is true, then  p is true in all possible worlds. p is true in all possible worlds. |
Another rule is what I’ll call “substitution:”
| In English | In Symbolic Logic |
|---|---|
|
p or q If q, then r ————— Therefore, p or r |
p 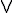 q qq  r r ————— 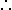 p p 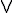 r r
|
Lastly, there is the modal version of modus tollens:
| In English | In Symbolic Logic |
|---|---|
| In all possible worlds: If p, then q —————— Therefore, If q is necessarily false, then p is necessarily false |
![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) (p (p  q) q)—————— 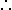 ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~q ~q  ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~p ~p |
![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~q
~q 
![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~p.
~p.
Now for the actual argument. Using the definition of God described earlier, let’s label the claim of “God exists” as G. Remember, in this case the theist defines “God” as “the greatest possible being.” Remember also that one argument for the first premise is that the greatest possible being would by definition have the greatest possible form of existence: necessary existence (if the being exists). If this is true, it logically follows that if God exists, he does so necessarily.
1. ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) (G (G  ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G) G) | The following statement holds true in all possible worlds: If God (on the definition above) exists, He exists necessarily. |
![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~G ~G | This states that G is not impossible, or  G. G. |
![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G G  ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~ ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G G | Becker’s postulate applied to ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G G
|
Those are the most disputable of the premises. The next two must be true by the rules of logic. (Becker’s postulate may be quite reasonable, but it hasn’t actually been proven in any rigorous sense.) Below is justification for the third premise:
This application of Becker’s postulate can be translated to read that, “If it is not the case that G is true in every possible world, then ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G is true in all possible worlds.” This premise is correct because if indeed G is not true in all possible worlds, then in each possible world the statement “G is not true in all possible worlds,” would in fact hold true.
G is true in all possible worlds.” This premise is correct because if indeed G is not true in all possible worlds, then in each possible world the statement “G is not true in all possible worlds,” would in fact hold true.
4. ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G G  G G | If God necessarily exists, then he exists. |
5. ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G G 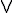 ~ ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G G | Law of Excluded Middle |
6. ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G G 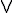 ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~ ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G G | 3,5 substitution |
7. ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~ ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G G  ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~G ~G | 1, modal modus tollens |
8. ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G G 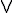 ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~G ~G | 6,7 substitution |
9. ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G G | 8,2 disjunctive syllogism |
| ——————————— | |
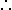 G G | 9, 4 modus ponens |
One question that might be raised is, “Could this reasoning prove any possible proposition?” That is, could it prove any possible statement (call it  p) to be necessarily true (i.e.
p) to be necessarily true (i.e. ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) p) and thus be actually true (i.e. p)? No. Premise #1 is true (allegedly) due to the at least somewhat unique nature of the proposition G. G is “the greatest possible being.” The greatest possible being would by definition have the greatest form of existence possible: necessary existence. Thus, if God exists he necessarily exists (or, G
p) and thus be actually true (i.e. p)? No. Premise #1 is true (allegedly) due to the at least somewhat unique nature of the proposition G. G is “the greatest possible being.” The greatest possible being would by definition have the greatest form of existence possible: necessary existence. Thus, if God exists he necessarily exists (or, G 
![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G). However, the structure of p
G). However, the structure of p 
![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) p does not hold true for just any proposition. For example, let N equal “I was born with No arms.” But if N is true, that doesn’t mean that N is true in all possible worlds, which is allegedly unlike God (when “God” is defined as “the greatest possible being”).
p does not hold true for just any proposition. For example, let N equal “I was born with No arms.” But if N is true, that doesn’t mean that N is true in all possible worlds, which is allegedly unlike God (when “God” is defined as “the greatest possible being”).
In substituting the premise “it is possible that God does not exist” we get a reverse ontological argument, i.e. an ontological argument that says God does not exist. This argument I thought up (though it turns out I wasn’t the first one) attacks the symbolic logic form of the ontological argument . At this time, I believed that “It is possible for God to not exist” (two symbolic forms:  ~G and ~
~G and ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G) was just as reasonable as as “It is possible for God to exist” (two symbolic forms:
G) was just as reasonable as as “It is possible for God to exist” (two symbolic forms:  G and
~
G and
~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~G).
~G).
Once we replace premise #2 with ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G, we can get
G, we can get ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G. To do this, we use ~
G. To do this, we use ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G together with line #8 and then using disjunctive syllogism, which gets us “God necessarily does not exist” (or in symbolic form:
G together with line #8 and then using disjunctive syllogism, which gets us “God necessarily does not exist” (or in symbolic form: ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~G) on line #9. Because I believed there isn’t any logical reason to favor ~
~G) on line #9. Because I believed there isn’t any logical reason to favor ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~G over ~
~G over ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G, I believed I proved the argument defective since switching ~
G, I believed I proved the argument defective since switching ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~G (premise #2) could be easily switched with ~
~G (premise #2) could be easily switched with ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G to logically prove that God does not exist.
G to logically prove that God does not exist.
Then I realized (two days later) a good response that a defender of this ontological argument might make: that line #9 wouldn’t make any logical sense once premise #2 was switched with ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G (because line #9 would then become
G (because line #9 would then become ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~G).
~G). ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~G means that God (the greatest possible being) necessarily does not exist, which means that G does not hold true in any possible world. Put another way,
~G means that God (the greatest possible being) necessarily does not exist, which means that G does not hold true in any possible world. Put another way, ![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) ~G can be translated to mean, “The greatest possible being cannot possibly exist,” which is absurd because of its self-contradictory nature given the coherent, meaningful definition of God. (Confer this paragraph before moving on to see what I’m talking about, then click the back button.) If a being is possible (e.g. the greatest possible being) it can’t be impossible. Consequently, the greatest possible being would by definition exist in at least one possible world. So switching premise #2 with ~
~G can be translated to mean, “The greatest possible being cannot possibly exist,” which is absurd because of its self-contradictory nature given the coherent, meaningful definition of God. (Confer this paragraph before moving on to see what I’m talking about, then click the back button.) If a being is possible (e.g. the greatest possible being) it can’t be impossible. Consequently, the greatest possible being would by definition exist in at least one possible world. So switching premise #2 with ~![[]](https://www.angelfire.com/mn2/tisthammerw/images/square.gif) G doesn’t and can’t prove that God does not exist because of the law of noncontradiction. So one reason
G doesn’t and can’t prove that God does not exist because of the law of noncontradiction. So one reason  G is favorable to
G is favorable to  ~G in this argument is that
~G in this argument is that  G doesn’t lead to a contradiction within any of the lines in the argument, unlike
G doesn’t lead to a contradiction within any of the lines in the argument, unlike  ~G. Another reason is that
~G. Another reason is that  G logically must be true (again, unlike
G logically must be true (again, unlike  ~G), because “the greatest possible being” is by definition possible given its coherent meaning. As a result, it would be a contradiction to say that the greatest possible being isn’t possible, whereas it wouldn’t break any rules of logic to say that it’s impossible for
~G), because “the greatest possible being” is by definition possible given its coherent meaning. As a result, it would be a contradiction to say that the greatest possible being isn’t possible, whereas it wouldn’t break any rules of logic to say that it’s impossible for  ~G to be true.
~G to be true.
|
Gaunilo (who was a monk of Marmoutier and a contemporary of Anselm’s) criticized Anselm’s argument saying that one could apply the statement to a lot of things, the most famous example he used was, “the greatest conceivable island” and prove the existence of the island using parallel reasoning of Anselm’s ontological argument. Similar to the ontological argument, we slightly modify the definition Gaunilo’s island to mean “the greatest possible island” instead of the original “the greatest conceivable island.”
“Proving” the existence of Gaunilo’s island can be done by replacing God with that island in the ontological argument. In his own words (in In Behalf of the Fool):
Now if someone should tell me that there is such an island [an island that which no greater can be conceived], I should easily understand his words, in which there is no difficulty. But suppose that he went on to say, as if by a logical inference: “You can no longer doubt that this island which is more excellent than all lands exists somewhere, since you have no doubt that it is in your understanding. And since it is more excellent not to be in the understanding alone, but to exist both in the understanding and in reality, for this reason it must exist. For if it does not exist, any land which really exists will be more excellent than it; and so the island already understood by you to be more excellent will not be more excellent.”
Gaunilo’s criticism applied below:
Conclusion: Statement 7 is absurd. It can’t possibly be true because it is self-contradictory. Therefore, Gaunilo’s Island must exist in reality as well as the mind.
I also thought of applying Gaunilo’s criticism to the symbolic logic argument. Using the same sort of reasoning, I believed I could “prove” all sorts of absurdities. Suppose, for instance, we used “the Greatest Possible Chicken” (GPC) instead of God. We could use parallel reasoning for the justification of the first two premises in the symbolic logic approach.
Using the same structure as the symbolic logic argument but using GPC instead of G (where G = God) we can prove the existence of this divine chicken. The same sort of thing could be used for “the greatest possible hot dog,” “the greatest possible sock” or even the “greatest possible pile of crap.” But this is nuts. Something has to be wrong here, and I believed that thing was the ontological argument. (Later, I e-mailed Tom Morris, author of Philosophy for Dummies, about this criticism. He e-mailed me a good rejoinder that a defender of the ontological argument would use on April 1 2002, and it’s the last response in the next section.)
|
One response is that Anselm’s ontological argument only applies to the greatest possible thing. It’s not absurd to believe that something greater than the greatest possible island exists (e.g. an intelligent person) but that would not be the case for God, a being that is the epitome of maximum possible perfection. God is that which nothing (and no being) greater is possible. So, unlike the island, it would be absurd to think that something is greater than the greatest possible thing.
Another response is that there is no limit to how great an island can be. The properties that contribute to the greatness of an island have no intrinsic maximum (borrowing the term from philosopher C. D. Broad). For any great island, there is another that could be greater. The “greatest possible island” is thus like, “the greatest possible integer.” No such thing can possibly exist because neither has an intrinsic maximum.
One could also remark that the characteristic of necessary existence does not seem to be one that an island could possess. After all, an island is a compound physical object (unlike God) and compound physical objects are contingent things. It is possible for them to be destroyed by falling apart or dropping a really big bomb on it.
Yet another response is that the notion of a “greatest possible island” isn’t all that coherently meaningful for an ontological proof that was used for God, and so the parallel is misleading. For instance, what would a greatest possible island (or chicken, pile of crap etc.) be like? How many leaves would the island have? How many feathers would the chicken have? How loud would the chicken cluck? How loud would the island’s creatures be? In principle, there are no answers to these questions, and thus things like “the greatest possible island” and “the greatest possible chicken” are not legitimate concepts, just as “the greatest possible integer” is not a legitimate concept (but for a different reason than the previous objection). This is because there isn’t anything that makes for greatness in islands, chickens and the like; it’s all a matter of taste. Truly objective standards of greatness for these sorts of things simply do not exist. There is nothing inherent in the definition of “island” and “chicken” that entails such perfection that was used when the argument described God. Thus, it isn’t so much as possible that there really be a greatest possible island. The concept of an island (sock, crap etc.) does not inherently include the notion of supreme perfection, instead the vague aspect of “perfection” is artificially pasted on to the core concept, while the concept of God (maximal perfection, “that which nothing greater is possible”) cannot be separated from its hardcore intrinsic meaning: maximal perfection. With God there is only one clear and coherent concept of maximal perfection, and so the argument that flows forth from this can’t be used to support any other concept. What about God? Aren’t his attributes of greatness subjective? Not at all. One way the theist could justify defining God as maximal perfection is to look at the summary property of God’s attributes. God is perfectly powerful, perfectly good, perfectly wise, perfectly knowledgeable, and so forth. Being perfectly powerful (omnipotence) for instance, is an objective quality. Or one can put this in terms of questions asked on the aspects of God. For instance, how much power does God have? Perfect power: omnipotence (to the greatest possible extent). How much knowledge does God have? Perfect knowledge: omniscience (to the greatest possible extent) etc. These questions have legitimate and objective answers and thus God (as defined here) is a legitimate concept, unlike the greatest possible island/number/chicken etc.
|
You might have seen this objection coming when you saw the one of the responses to Gaunilo’s Island. This objection says that the concept of God is like the greatest possible integer. There is always one greater. God (as defined in this ontological argument) is an incoherent concept, and possesses no adequately coherent meaning because there are no intrinsic maximums. Incidentally, C.D. Board himself brought up this objection when he used the term intrinsic maximum. Note also that the justification for the “God is possible” premise presupposes that it is working with intrinsic maximums. If this objection is correct, then the justification for that premise fails.
It would seem that there are intrinsic maximums for the qualities of God. For instance, God’s omniscience can be defined as knowing everything that can be known, and God’s omnipotence can be defined as being able to do anything that can be done. There aren’t any greater possible conditions for those aspects of knowledge and power. They are intrinsic maximums.
Immanuel Kant (1724-1804), the very same 18th century German philosopher who first called the argument “ontological,” made this objection. This criticism attacks premise 3 in the reductio ad absurdum approach and the justification made for premise #1 in the symbolic logic argument. It has been widely accepted among philosophers who reject the ontological argument. A predicate is a property we attribute to something. For example, a red strawberry has “red” as one of its predicates. In a sentence, a predicate is used to denote additional information about the subject. In Kant’s own words (and in his book, Critique of Pure Reason):
Being is evidently not a real predicate, that is, a conception of something which is added to the conception of some other thing. It is merely the positing of a thing, or of certain determinations in it. Logically, it is merely the copula [i.e. the verb linking the subject and the predicate] of a judgment. The proposition, God is omnipotent, contains two conceptions, which have a certain object or content; the word is, is no additional predicate—it merely indicates the relation of the predicate to the subject. Now if I take the subject (God) with all its predicates (omnipotence being one), and say, God is, or There is a God, I add no new predicate to the conception of God, I merely posit or affirm the existence of the subject itself, with all its predicates, in relation to my concept, as its object.
There is a difference between predicating something (e.g. “this person is tall”) and saying something exists. Consider the list of predicates below:
But existence merely says, “God is.” As for the word is, it is only a copula (i.e. a verb that links the predicate with the subject). It is not a predicate itself. Unlike real predicates, existence doesn’t say anything about what God is like (e.g. omnipotent, perfectly good, etc.), only that God is. Existence as a predicate is meaningless to use because, according to Kant, it tells us nothing about the subject (confer calling a strawberry “red” or a person “tall”).
One interesting response is that it doesn’t matter if existence is a predicate or not. Another line of justification could be used. Necessary existence is certainly a predicate (hence its use as a predicate in predicate logic), even if existence per se is not. Necessary things are greater than contingent things since they cannot fail to exist. Imagine two things, the first which exists contingently and the second which exists necessarily (all other aspects are identical). Is not the second greater or more perfect than the first? Therefore, if God exists He exists necessarily (thus supporting premise #1 in the symbolic logic approach), because necessary existence is greater than contingent existence.
Kant’s justification for existence not being a predicate seems unsound. He claims that existence is merely the copula for the predicate and the subject, such as the word is in “God is omnipotent,” and any other form of “[subject] is [predicate].” Suppose that existence is just the copula. If that were true, then attaching a predicate to a subject with the copula would presuppose the subject’s existence. But we predicate non-existent things all the time. Suppose I say, “Santa Claus is a jolly fat guy.” I really don’t mean to imply that Santa actually exists when I describe him.
|
A related response is that existence does seem to be a predicate. Suppose an inquiring child who has always believed that Santa Claus existed asks me if this is so. I tell the child that Santa Claus does not exist, and the child believes me. The objection of existence not being a predicate would seem to say that the child has not learned anything new about Santa Claus, but surely that is a bit peculiar. To say that the child has not learned anything new about Santa Claus when the child learns of Santa’s nonexistence seems dreadfully nonsensical. When a mathematician says that there exists prime numbers between 12 and 21, is she not denoting a characteristic of prime numbers? The objection would again seem to say no. But clearly the child has learned something about Santa Claus, and the mathematician has mentioned a characteristic of prime numbers. Thus, existence does seem to be a property one can attribute.
|
Because Kant believed existence is not a predicate, he believed that existence is not a great-making predicate. This objection focuses on the claim of existence not being a great-making property and says that the reason “the greatest possible island,” and “the greatest possible chicken” don’t work as arguments to prove their respective existences is because “existence” doesn’t actually make something greater. To use another example, is the existence of Stalin, the Devil, Hitler, and maniacal mass murderers (say that three times fast) greater than their failure to exist? Obviously not. This is because existence is not a “great-making” property.
Maybe existence doesn’t make things like maniacal mass murderers great, but it seems to make some other things great, like mountains, beauty, or God. All else held constant, beauty that exists is greater than beauty that does not exist. Similarly, an existing God is greater than a non-existing God.
|
|
Do the responses satisfactorily answer the objections? Is the concept of greatest possible perfection sufficiently unique to the definition of God? Is this concept of perfection properly meaningful for the first premise to be true? To be honest, I’m still not entirely sure what to make of it all. How about you?
|
