En esta sección revisaremos algunos ejemplos de cómo aplicar la derivada. En situaciones del mundo real, como hemos mencionado, hay ocasiones que nos vemos en la necesidad de encontrar la razón de cambio o la velocidad de una magnitud. Por lo que debemos derivar la función que describe la magnitud. A continuación te presentamos una tabla con las principales reglas de derivación:

Derivadas

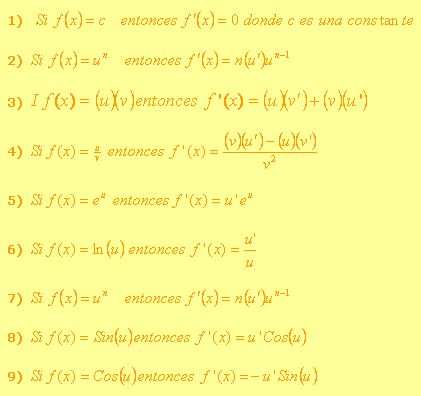Vamos a revisar los siguientes ejemplos:

Ejemplo 1. Un objeto tiene una ecuación de posición dada por . Encuentra la ecuación que da cuenta de su velocidad y la ecuación para su aceleración.

Solución: Como nos piden la velocidad, necesitamos calcular la derivada. Revisando la función observamos que se trata de una función polinomial, por lo que necesitamos utilizar las reglas de derivación 1) y 2) para potencias y constantes. Por lo tanto aplicando las reglas:

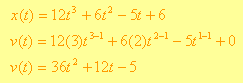
Para obtener la aceleración, recordemos que se trata de la razón de cambio de la velocidad por lo que debemos de derivar la ecuación de velocidad obtenida:

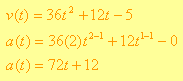
Ejemplo 2. Una población está creciendo de acuerdo a la ecuación , encuentra la razón de cambio de la población.

Solución: Como se nos pide la razón de cambio, debemos encontrar la derivada utilizando las reglas de la tabla, en este caso la regla 5) para funciones exponenciales en donde debemos de identificar la u que en este caso es el exponente de la función:

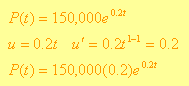
Puedes utilizar los siguientes ejercicios para practicar.

Resuelve los siguientes ejercicios de aplicaciones de derivadas, en todas las situaciones es necesario usar la derivada para encontrar la razón de cambio o la velocidad.

Problema 1. Una taza de café se calienta en un horno de microondas y alcanza una temperatura de 80 ° C. La taza de café se extrae del horno y se expone al medio ambiente que se encuentra a una temperatura de 20 ° C. El tiempo t (medido en minutos) se empieza a registrar a partir de este momento.

Para todo fin práctico podemos considerar que la ecuación que nos calcula la temperatura en cualquier instante t , dentro de los primeros 5 minutos, está dada por: T ( t ) = 80 – 3 t + 0.16 t 2

Obtén la razón de cambio de la temperatura con respecto al tiempo (la derivada).

Problema 2. Consideremos a la siguiente situación de la caída libre de un cuerpo:

Un objeto se deja caer desde lo más alto de un edificio. En lugar de empezar a medir el tiempo cuando el objeto se deja caer desde la azotea (como lo hemos hecho usualmente) lo empezaremos a medir cuando el objeto pasa por la ventana de uno de los pisos. En ese momento el objeto viaja a una velocidad v 0 = 4 m/seg y es visto por un observador que se encuentra a una distancia s 0 = 5 me de la parte superior del edificio.

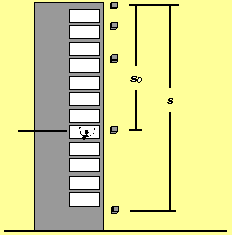Bajo estas circunstancias se puede probar que la distancia total recorrida queda expresada en términos del tiempo mediante la fórmula:

a) Obtén la fórmula de la velocidad v ( t ) del cuerpo. (La derivada).

b) Calcula la velocidad en el instante t = 3 segundos.

Problema 3. Un objeto tiene un movimiento descrito por la ecuación

a) Encuentra la ecuación de velocidad (derivada).

b) Encuentra la ecuación de aceleración (derivada de la velocidad)

Problema 4. LA LEY DE BOYLE.

Cuando una cantidad fija de gas se encierra en un depósito cuyo volumen puede agrandarse o achicarse, la ley de Boyle nos dice que (a temperatura constante) la presión P que ejerce el gas encerrado sobre la pared interna del depósito (medida en kilogramos por centímetro cuadrado, por ejemplo) es inversamente proporcional al volumen V del depósito. Esto es

Supongamos que en t = 0 el volumen del depósito es 50 cms3 y la presión que ejerce el gas encerrado es de 10 kgs/cm2.

a)¿Cuánto vale la constante c de la ecuación ?

Supongamos además que el volumen empieza a aumentar a partir de t = 0 y que en el instante t = 10 segundos, el volumen es V = 100 cms3 y está aumentando a razón de 5 cms3/seg.

b) ¿Cuál es la presión P que ejerce el gas encerrado en el instante t = 10 segundos?

c) ¿A que razón está cambiando la presión P con respecto al tiempo en t = 10 segundos?

Sugerencia para c) :

Calcula a partir de la fórmula usando la fórmula para derivar un cociente. Utiliza el valor de c calculado en el inciso a).

Problema 5. La ecuación de posición de un móvil es:

x ( t ) = 10 t e -3 t

x se mide en metros y t en segundos. Obtén la velocidad del móvil en t = 3 segundos.

Las siguientes ligas te ofrecen otros ejercicios adicionales:

http://ciencias.bc.inter.edu/ntoro/calculo/velocidad.htm

http://www.mundofree.com/fsanchezf/derivada.htm