How can you tell where something is with only an address given? Can you find distances given two addresses?
type: tip
reliability: 
- medium
understandability: 
- medium-high
time saving: 
- small loss
usefulness: 
- very high
difficulty: - easy-medium
required skill: 
- novice
overall: 29 of 48 points,
Addresses, particularly the US addresses can tell you location and can be used to calculate distances. So, the next time you need to go driving around in you home town, take note of the street and avenue signs that tell you what street or avenue you're on. To explain, before we get into answering the question on distances between points, let's get the basics down first.
1. The coordinate graph
Try this once, take out your home town's city map. This can be found in your home town's phonebook or via Mapquest. Ever notice that all street and avenue numbers increase as you get further and further from the city's center? City center is defined as the point in which main street and central avenue intersect. On a coordinate graph, this would resemble the point (0,0), which is also called the origin. Look at your city map once. Find where Main Street and Central Avenue meet up at the intersection. We'll call this point (0,0). If you head north, the avenue numeric names increase. If you go south from the center, the values increase as well. East and West is where your Street values increase as you head away from city center.
Just for an example, picture a coordinate graph. At the center is where the x and y axes meet. If you go up on the coordinate graph, the y coordinate increases into the positive range, but go down and it increases in the negative range. Go right it increases positive and left for negative. Now note the same pattern with a city map. Addresses never use negative numbers [or I haven't seen one yet].
Next, note that there are four possible "extentions" to the address, NE, SE, SW, and NW. These are called "quadrants". Quad-, meaning four, gives you the hint. Though, addresses have something odd that the coordinate graph doesn't. When naming a point, say (3,-4), the x and y axes are reversed in addresses.
Let's try to find the point (3,-4). In all ordered pairs, the x-axis is first, the horizontal one. If it's positive, you go right from the origin, but left if it's negative. Since that 3 is positive, you move right 3 points on the graph. The second coordinate is the y-axis, the vertical one. Go up if the value is positive and down if negative. -4 means to go four points down from the origin.
2. Coordinates as an address
This same principal works with addresses. The types of addresses that can be used for this trick to work are always in the format of 300 4th [street or avenue] [quadrant]. Let's take an example address of any city, 300 4th Street SE. Because "4th street" is already defined, the avenue's value doesn't exist yet. Though, if you remove the last two digits on the unnamed value, you get 3, which means 3rd avenue. Because street is previously defined. Note the quadrant, which can be of NE, SE, SW, or NW [or, on some addresses, just N, E, W, or S, but only if on main street or central avenue]. This means that this key location is in the SE quadrant. Find where 4th street and 3rd avenue intersect in the SE quadrant and that's the key location of your targetted destination.
You're not finished yet! Because of the fact that 4th street is already defined, you need to drive along 4th street where 3rd avenue is away from city center. If you're drivin' down a residential area and look at the house numbers, you may see something like 300, 302, 304, 306, ..., 318, 320, 400, 402, etc.. The number has changed to the 400 series because you just passed by 4th avenue. Continuing on, it may be 418, 420, then 500 when you pass the 5th avenue intersection.
If you were to picture a city map as a coordinate graph, you'd see something as this image demonstrates:
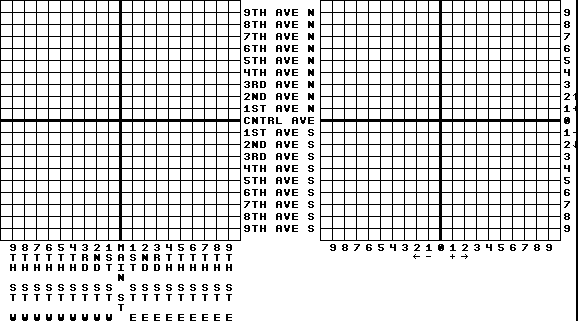
Do you see how closely addresses are related to a coordinate graph?
If you'd like to pinpoint the exact location more easily, the two dropped digits answer this. The address, 300 4th Street SE is just a bit to the east of where 3rd avenue and 4th street intersect in the SE quadrant. If the address was something like 308 4th Street SE, you'd head east a bit further from where 3rd avenue and 4th street intersect in the SE quadrant, but before 4th avenue comes.
Try this: if your home's address follows this same principal, in the US, apply this method then find it on your city map. Try it with your work place or school [you may have to find the address in your local phone book].
3. Finding distances
Because of the fact that addresses are related to a coordinate graph, you can easily calculate your distances. Let's say you want to travel from 600 4th avenue NE to 300 7th street NW. The first thing you need to do is convert the addresses into an ordered pair. The first thing to doing this is to break up the address into 3 parts, the avenue part, which is already defined, the street, which is indirectly defined, and the quadrant. The first thing to do is to define the streets and avenues, which should be easy to do. Unlike a coordinate graph, the y-axis is not always mentioned first. To be safe, always list the street value first. Next, find where the start destination is, which is 600 4th avenue NE. Remember, if the avenue is already defined, the other one, street, is what the first number is. If street was defined, the number is the street value. After finding this, find the target destination's location, then give their locations on the coordinate graph. 600 4th avenue NE is the same as (6,4). Remember, avenues increase as you head north or south from city center. The other address, your target destination, is 300 7th street NW, which converts to (-7,3). Remember, W and S are of negative numbers while N and E are of positive numbers. Third, subtract both x-axes. 6--7 is 13. When you subtract a negative number, change it to adding a positive number. To get from (6,0) to (-7,0), you travel 9 units left. Next, subtract your y-coordinates. 4-3 is 1 as the distance from (0,4) to (0,3) is 1 unit. Finally, add your two values and that's the road distance you travel, or 14 units. In addresses, every 12th marker is one mile exactly, or 440 feet per intersection [it may vary, and doesn't include halves]. To find the direct distance, you need to use the Pythagorean Theorum. First, find the difference between the two x coordinates [13 in the example] then the two y coordinates [1 in the example]. Square each [by multiplying them by itself; 132=169; 12=1] and add your squared values [169+1=170]. Finally, take the square root of this answer and that's the most direct distance [170.5 is just over 13 intersections, or just about 1 1/12 miles].
Try this with your home and your work place or school. This assumes that there are no curves, including hills. Then, when you're driving to work, or riding with your parents to school, check the odometer. You'd be amazed to how accurate this can be.
I don't even know where much of anything is around my home town, however, given an address in the usable format, I can find just about any place, no matter how remote it may seem!
4. The unfortunate weaknesses
This trick has it's weaknesses though. The first one is if the address doesn't have these two sets of numbers and specially named. An example is 1403 Spice Avenue SW. Because the special name "Spice" is used, you cannot figure out the distance without using a city map to estimate the coordinates of it.
The second weakness, which is quite obvious, is when curves are involved and the fact that not all streets are spaced evenly. Ever notice half streets or half avenues? This is due to the fact that they are spaced out half the normal distance between streets and avenues, or 220 feet.
The third weakness deals with foreign countries especially those that use something completely different or use metrics instead. If metrics are used, but the same principal is used, the method is also just as effective, only with some slight changes.
A fourth and final weakness is that it doesn't work for measuring between cities as the values reset when you approach the next city.
Besides these four weaknesses, this method works quite well and can be very reliable and useful.
Footnotes:
There are no footnotes for this page.
