Figure 0.1 Schematic Diagram of a Flashlight.
For a verbal description click here.
Chapter 0 Electrical Fundamentals.
0.1 Electrical Quantities From Mechanical Quantities.
0.2 Resistance and Ohm's Law.
0.3 Series Circuits and Kirchhoff's Voltage Law.
0.4 Parallel Circuits and Kirchhoff's Current Law.
0.5 Prefixes.
0.6 Numerical Examples.
0.7 Capacitance.
0.8 Inductance.
0.9 Problems.
0.10 Answers to Problems.
Chapter 0.
Electrical Fundamentals.
This chapter is intended as a review of material which the student should be familiar with. If the student is not familiar with the material in this chapter, intensive study of this chapter may not be sufficient. A review of textbooks used in previous courses may be required.Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
0.1 Electrical Quantities From Mechanical Quantities.
Electric Charge.
It is difficult to say exactly what electric charge is but you are all familiar with it. You walk across the carpet on a cold winter morning, reach for the doorknob and - ZAP - you get an electric shock. Your body acquired the property of electric charge by friction with the carpet.Electric charge can be placed on objects under somewhat more controlled circumstances. One way is to rub a rubber rod with a piece of cat's fur. The rod will now attract small objects such as bits of paper. The charge on the rod induces the opposite charge on the bits of paper. The fur will also attract small objects but it is not as easy to handle as the rod.
The property of electric charge will cause two bodies which possess a charge to exert a force on one another. The magnitude of this force is directly proportional to the amount of charge on each body and inversely proportional to the square of the distance between the two bodies. In equation form this law is
F = q1 q2 / r2 (0.1) where F is the force in Newtons, q1 is the amount of charge on body 1, q2 is the amount of charge on body 2 and r is the distance between the two bodies in meters.
If the distance is 1 meter and the force is 1 Newton and the two bodies have the same amount of charge, the amount of charge on each body is 1 coulomb. This is the definition of a coulomb, which is the unit of charge in the MKS system.
If the two bodies have charges of the same sign, the force is repulsive. If the two bodies have charges of opposite sign, the force is attractive.
The charge on one electron is 1.601864 x 10-19 coulombs. Therefore, one coulomb of charge is equal to the total charge of 6.24 x 1018 electrons.
In terms of mechanical units the dimensions of a coulomb are
Coulombs = Meters x Newtons1/2 (0.2)
Electric Current.
Electric current is the motion of electric charge through any conducting material. When a direct current is flowing in a wire, electrons are in continuous unidirectional motion along the wire.Current expresses the amount of charge per unit time passing a given point on a conductor. One way of defining current would be to specify the number of electrons per second passing a point. Although this would be a perfectly valid way of specifying the amount of current in a conductor, the numbers which would result in practical applications would be so large as to be unwieldy. More practical numbers result if the coulomb is taken as the basic unit of charge instead of the electron.
The most commonly used unit of current is the ampere. One ampere is equal to one coulomb of charge per second passing a point on a conductor. Thus the basic units of current are
Amperes = Coulombs / seconds (0.3) If desired the mechanical units of charge could be substituted into this equation and a strictly mechanical definition of current could be obtained. This is left as an exercise at the end of this chapter.
The symbol I is used for steady-state currents while the symbol i is used for time-varying currents.
The mathematical equations which relate current, charge and time are
I = Q / t (0.4) or
I = dq / dt (0.5) The use of an upper-case letter for steady-state values and the lower-case equivalent for time-varying values is common practice in electricity and magnetism.
Conventional Current.
When an electric current moves through a circuit, the negatively charged electrons flow toward the positively charged part of the circuit. This means that electrons come out of the - side of a battery and go into the + side.Physicists and electrical engineers alike prefer to use conventional current instead of electron current. Conventional current does what you would expect it to do. It flows out of the + side of a battery and flows into the - side.
Some students find this confusing. If you are among the confused, try this. Never think about electron current. Banish electron current forever from your mind and think only in terms of conventional current.
If any one man can be blamed for this confusion it seems to be the fault of Benjamin Franklin. Everyone knows about his "kite in the lightning storm" experiment. What few people know is that Dr. Franklin wrote one of the first if not the first textbook on electricity. He assembled all that was known at that time about electricity and put it in one book. He seems to have added very little in the way of original work himself but one thing he did add was a sign convention for electric charge. The convention he chose was a guess and he guessed wrong. Just think of it, if he had guessed the other way, we would have positive electrons and conventional current would be the same as electron current.
Electrical Potential.
Mechanical potential is expressed in units of work- energy. Electrical potential also is an expression of work which can be done or energy stored. The units are work per unit charge. If work is done on a given amount of charge, the potential has increased. If the charge does work the potential has decreased.Electrical potential like mechanical potential has no absolute zero. Electrical potential is always expressed as a potential difference between two points. In some cases one of the points is implied or understood in context. Electrical potential is meaningless unless two points are specified, implied, or understood.
Because potential is specified between two points the term potential difference is often used. The "difference" is usually omitted when speaking and often omitted when writing; "potential difference" is always understood by speaker, listener, writer and reader.
The unit of electrical potential difference is the volt. Potential difference is often called the voltage difference or the voltage drop but most often just the voltage.
If one joule of work is done on one coulomb of charge, the charge is moved through a potential difference of positive one volt. If one coulomb of charge does one joule of work, the charge has moved through a potential difference of minus one volt.
The basic units of voltage difference are
volts = joules / coulomb (0.6) As with units of current, the mechanical units of charge could be substituted into equation 0.6 to obtain purely mechanical units of voltage difference.
The term "electromotive force" was once regularly used to describe electrical potential difference. This led to the use of the symbol emf and later to the letter E to symbolize potential difference. In more recent times the letter V has been adopted for drops across passive components. The letter E will be used for the voltage of energy sources. This convention will be used throughout this book. The equations for voltage in terms of more basic units are
V = W / Q (0.7) or
dv / dt = dw/dt / Q (0.8) Charge is not indicated as being time-varying because it is conserved. Charge can neither be created nor destroyed.
Electrical Power.
In mechanics, power is the rate of doing work or work per unit time.Power = work / Time (0.9) Electrical power is no different. Electric power is
Power = Current x Voltage. (0.10) If we substitute the mechanical units of voltage and current into equation 0.10 we have
Watts = Coulombs / Second x Joules / Coulomb = Joules / Second (0.11) Thus
P = I x V (0.12) Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
0.2 Resistance and Ohm's Law.
An Electric Circuit.
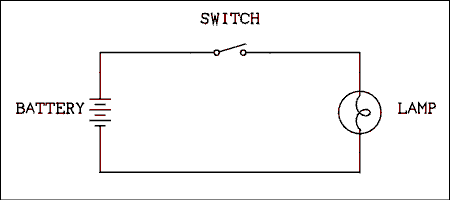
In order for electricity to be useful, it must be harnessed to do work for us. The usual way of making electricity do work is to connect a source of electric energy to a device which converts the electric energy into another useful form of energy. An example of this is the flashlight, the schematic diagram of which is shown in figure 0.1.

Figure 0.1 Schematic Diagram of a Flashlight.
For a verbal description click here.
The battery on the left converts chemical energy into electrical energy. The lamp on the right converts the electrical energy into electromagnetic energy, some of which is in the visible light part of the electromagnetic spectrum. The switch is used to interrupt the flow of electrons and permit the light to be turned on and off. The lines on the drawing indicate conductors such as wire which normally have negligible amounts of resistance compared to the rest of the circuit.Resistance.
When an electric current flows through a very good conductor, such as a copper wire, the electrons move very easily and very little work is required to move them. A copper wire has very low, almost zero resistance.When an electric current attempts to flow through a very poor conductor, such as a piece of glass or the open switch, a near infinite amount of energy would be required. In purely practical terms, electrons do not move through pieces of glass or open switches and there is no current flow. No current flow means that no charge is moved and no work is done. A piece of glass or an open switch has very high, almost infinite resistance.
When an electric current flows through a thin wire such as the filament in the lamp, the electrons can be moved but considerable work is required to make the electrons move. The filament of a lamp and other devices on which electricity does work are said to have finite resistance.
Current, Work and Potential.
If the current flows through a part of the circuit which has zero resistance (a super conductor) no work is required to move the electrons through this part of the circuit. Electric charge is being moved but no work is being done. In as much as potential difference (voltage) is defined as work per unit charge (equation 0.6) if the work is zero, the voltage is zero.If the current flows through a part of the circuit which has a finite resistance, work is required to move the charge. If work is done, there is a potential difference across that part of the circuit. If the amount of charge per unit time remains constant, doubling of the amount of resistance will cause the amount of work to be doubled and the voltage to be doubled. Therefore, the voltage is directly proportional to the resistance.
If we now hold the resistance constant and allow the current (charge per unit time) to vary we discover the following. If the current doubles, there is twice as much charge to be moved and twice as much work will be required to move it. Which leads us to the conclusion that the voltage is directly proportional to the current.
We have now concluded that the voltage is directly proportional to the current and the resistance. As we saw at the beginning of this discussion, if the resistance is zero, the voltage is zero. On the other hand if the resistance is finite and the current is zero, there are no charges to do work on and there can be no potential difference. This is a strong indication that voltage is proportional to the product of resistance and current.
V = I x R (0.13) Resistance is defined in terms of volts and amps as follows. If a current of 1 ampere is flowing through a resistance of 1 ohm, the voltage which results will be 1 volt. Even the ohm can be defined in terms of purely mechanical units.
The above discussion is as close as we can come to a derivation of Ohm's law (equation 0.13). In fact Ohm's law was discovered experimentally and is strictly an empirical law.
Resistance and Power.
It is important to know how much power is being dissipated in a resistor. Every resistor has a maximum power rating. If this power is exceeded, the resistor will get overheated and quite literally burn up. Whenever a resistor is put into service a power calculation should be performed to make sure that the resistor will not burn out.One way to make a power calculation is to multiply the current through the resistor by the voltage across it. This must be valid but if you know only one, voltage or current, you must use Ohm's law to calculate the other. A couple of shortcuts can be developed by combining equation 0.12 (power) with equation 0.13 (Ohm's law). A direct substitution of 0.12 into 0.11 gives
P = I x I x R = I2 x R (0.14) Solving Ohm's law for current and substitution gives
P = (V / R) x V = V2 / R (0.15) These equations should not be confused with the definition of power but they are often very handy.
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
0.3 Series Circuits and Kirchhoff's Voltage Law.
Electric circuits get much more complex than the flashlight shown in Figure 0.1. We will work our way up from simple circuits to more complex circuits.

Figure 0.2 Schematic Diagram of a Series Circuit.
For a verbal description click here.
A series circuit is defined as a circuit in which there is only one path to be followed from a given point, around the circuit and back to the same point. Figure 0.2 qualifies under this definition of a series circuit.In Figure 0.2 the letter E is used to symbolize the emf or potential difference across the battery. The symbol V1 is used for the potential difference across the resistor R1. In general the symbol VN will be used for the potential across any resistor RN.
Conventional current flows out of the positive terminal of the battery, through R1, through R2, through R3 and to the negative terminal of the battery. Current is symbolized by the letter I.
Current in Series Circuits.
Let us use the general symbol IN for the current in resistor RN and the letter I for the current in the battery. Remember that current could be expressed as the number of electrons per second passing a point in the circuit.As electrons move around the circuit, there are no side roads for them to take. Electrons cannot pile up at any particular place in the circuit. If there was a pile-up, the concentration of negative charge would repel additional electrons from that vicinity and the pile-up would soon be gone. Pile-ups never happen in the first place.
Because we have established that electrons cannot accumulate at any point or get out of the circuit at any point, we may say that the number of electrons per second passing any point in the circuit of Figure 0.2 is the same as the number of electrons per second passing any other point in the circuit. In other words the current at any point in the circuit is exactly the same as the current at any other point in the circuit. This can be stated in equation form as
I = I1 = I2 = I3 (0.16) Equation 0.16 is a consequence of Kirchhoff's current law although we don't officially know that yet.
Voltage in Series Circuits.
Remember that potential difference or voltage is work per unit charge. From mechanics remember: 1) the equivalents of work and energy, 2) the conservation of energy and 3) the conservation of charge. Also remember that the current in any resistor in Figure 0.2 is the same as the current in any other resistor and the same as the current in the battery.The amount of work done by the battery is equal to the sum of the work done on each resistor, In equation form
W = W1 + W2 + W3 (0.17) If we solve equation 0.7 for W and substitute into equation 0.17 we have
QE = QV1 + QV2 + QV3 (0.18) As the current is the same everywhere in the circuit, the charge per unit time is the same and all occurrences of charge are the same. The charge Q will cancel out. Thus we have
E = V1 + V2 + V3 (0.19) Equation 0.19 is a special case of Kirchhoff's voltage law.
Kirchhoff's voltage law states that the algebraic sum of all voltage drops around any closed loop is equal to zero. Thus, Kirchhoff's voltage equation for the circuit of Figure 0.2 is
- E + V1 + V2 + V3 = 0 (0.20)
Voltage Rises and Drops.
All voltages are really voltage differences. A potential difference or voltage difference can be either a voltage rise or a voltage drop. Although it may be stating the obvious, a rise is an increase in potential or voltage and a drop or fall is a decrease in potential or voltage. If we start at a particular point in a circuit and move around the circuit we may move from a point of low potential to a point of higher potential. We have traversed a potential rise. If we move from a point of high potential to a point of higher potential we have again traversed a potential rise. The starting point makes no difference; it is the change that is important. Similarly if we move from a point of any given potential to a point of lower potential we have traversed a potential drop or fall.For example, if we traverse the battery in Figure 0.2 from bottom to top, we have traversed a rise. Conversely if we traverse the battery from top to bottom, we have traversed a drop. From this you can see that a battery is not automatically a potential rise; it depends on the direction of travel.
It is easy to tell the direction of the potential or polarity of a battery because of the polarity markings. A battery will always have the same polarity (positive on the long line) regardless of whether it is being charged (current flowing into the positive terminal) or discharged (current flowing out of the positive terminal). The positive terminal of the battery is always positive no matter which way the current is flowing.
Resistors and other passive devices are another story. Conventional current always flows out of the most negative end of a passive device. Thus, the end where the current goes in is more positive than the end where the current comes out.
In solving Kirchhoff's equation it is very important to give the proper sign to each quantity. If an incorrect sign is given to a particular value, the result will be incorrect. Here are some rules to follow in writing Kirchhoff's equations.
- 1 Mark the polarity on all voltage sources (batteries) by placing a minus (-) sign next to the negative terminal (short line) and a plus (+) sign next to the positive terminal (long line).
- 2 Assume a direction for the current. Clockwise is a standard assumption used by those who solve circuit equations. Don't be concerned if you can't tell which direction the current is actually flowing. The numeric answer will have a sign which will tell us if the initial assumption was right or wrong.
- 3 Mark the polarity on all passive devices (resistors) by placing a plus (+) sign at the end where the current enters and a minus (-) sign at the end where the current exits.
Now that you have polarity markings on each part in the circuit you are almost ready to write a Kirchhoff's equation.
Do not be concerned about the fact that there are + and - signs next to each other on opposite ends of the same wire. The signs refer to that particular circuit element alone. The positive end is more positive than the negative and the negative end is more negative than the positive end. The signs say nothing about what the potential is with respect to other parts of the circuit.
Kirchhoff's law states that the sum of all voltage drops is equal to zero. It could just as well say that the sum of all voltage rises is equal to zero. The only difference between the two resulting equations will be that one has been multiplied through by -1 as compared to the other.
If you are summing the rises, a drop is a negative rise. A drop is the negative of a rise. Conversely a rise is the negative of a drop. Therefore, if we sum the drops, a drop is a positive quantity and a rise is a negative quantity.
Apply the three rules above to Figure 0.2 and start at the lower left corner. The battery E is a rise which is a negative drop. Thus we write a negative (- E) in equation 0.20. The drops across the resistors are just that and are entered as positive quantities.
Example 0.1.
Write Kirchhoff's voltage equation for the circuit of Figure 0.3.

Figure 0.3 Series Circuit With Multiple Voltage Sources.
For a verbal description click here.
Solution.
First, mark a + sign near the positive (long line) and a - sign near the negative (short line) of each battery. Indicate a clockwise direction for the current by drawing an arrow on the figure. Put + and - signs on each resistor as follows. The lower end of R1 is positive and of course its upper end is negative. The left ends of R2 and R3 are positive. The upper end of R4 is positive. Of course the other end of each resistor is negative. Now we can write the equation. Start at the lower left corner and move around the circuit in a clockwise direction. If we sum the drops we get- E1 + V1 + V2 - E2 + V3 + V4 + E3 = 0 (0.21) If we sum the voltage rises we get
E1 - V1 - V2 + E2 - V3 - V4 - E3 = 0 (0.22) Equation 0.22 is just equation 0.21 multiplied by -1. If we were to plug in numbers and solve them, both would give the same answer.
Resistors in Series.
Suppose we have three resistors in series as in Figure 0.4a and we wish to replace them with a single resistor as in Figure 0.4b. We want a single resistor Req which will cause the same amount of current to flow as the series combination of R1, R2, and R3, when connected across the same voltage source (battery). In other words we want one resistor which will act the same as the three resistors together.

Figure 0.4 (a) Three Resistors in Series,
(b) One Equivalent Resistor to Replace it.
For a verbal description click here.
We now apply a voltage E to the resistors as shown in Figure 0.5. Kirchhoff's equation is - E + V1 + V2 + V3 = 0. Solving for E givesE = V1 + V2 + V3 (0.23) The equivalent resistor Req would give the simple equation
E = Veq (0.24) If we substitute Ohm's law VN = I x RN and remember that the current I is the same everywhere in a series circuit we have
I x Req = I x R1 + I x R2 + I x R3 (0.25) canceling I
Req = R1 + R2 + R3 (0.26) and in the general form
Req = R1 + R2 + ... + RN (0.27) Equation 0.27 says that the equivalent of any number of resistors in series is the sum of all of the resistors in series.

Figure 0.5 (a) Three Series Resistors Connected to a Voltage
Source, (b) One Equivalent Resistor Connected to a
Similar Voltage Source.
For a verbal description click here.
Logical Checks.
In any problem-solving course it is a good idea to have in mind some rules of logic for checking answers. You should look at an answer and ask yourself "Does that answer make sense?" From time to time this book will give some common sense rules under the heading of "Logical Checks".When finding the equivalent of series resistors the equivalent will always be greater than the largest single resistor.
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
0.4 Parallel Circuits and Kirchhoff's Current Law.
A parallel circuit is defined as a circuit which has two or more independent paths which can be followed from a given point in the circuit back to the same point. A simple parallel circuit is shown in Figure 0.6.

Figure 0.6 Schematic Diagram of a Parallel Circuit.
For a verbal description click here.
Voltage in Parallel Circuits.
Now that we know Kirchhoff's voltage law let us use it. This law applies to any circuit as long as we go around a loop taking every voltage drop into account and coming back to the original starting point.In Figure 0.6 let us start at the lower left corner, go up through the battery, to the right to the top of R1, down through R1 and then back to the left to the starting point. The resulting equation is -E + V1 = 0 or E = V1.
Now let us follow a path through R2. Start at the lower left corner, go up through the battery, to the right to the top of R2, down through R2 and then back to the left to the starting point. The resulting equation is -E + V2 = 0 or E = V2.
The argument is the same for R3. Thus we have shown that
E = V1 = V2 = V3 (0.28) In a simple parallel circuit the voltage across any one element is the same as the voltage across any other element in the same circuit.
Current in Parallel Circuits.
Figure 0.7 is the map of a rather strange system of roads. The system is one-way, left to right. Cars are fed into the system at the left at a rate measured in cars/hour. At the first junction some cars go left, some go straight and some go right. The cars go through the three parallel roads and join up again at the rejoin point. Cars cannot get out of the system except at the ends and no cars from the outside can get in. Cars exit on the right at the same rate as they enter on the left. No stopping in the red zone.

Figure 0.7 Map of Strange Road System.
For a verbal description click here.
When the car-current (cars/hour) splits it is obvious that the sum of the car-currents (KN) in the three paths is equal to the car-current (K) in the main path.K = K1 + K2 + K3 (0.29) Look at Figure 0.6 and visualize the electrons in the circuit doing the same as the cars on the road. This is the justification for writing the equation
I = I1 + I2 + I3 (0.30) which is a special case of Kirchhoff's current law.
Kirchhoff's current law says that the sum of all currents flowing into a junction is equal to zero. If current going in is defined as positive, then current coming out is negative.
In Figure 0.6 the top line is a junction where currents may be summed and the bottom line is another junction where currents may be summed. If we sum the currents in the top line we have
I - I1 - I2 - I3 = 0 (0.31) if we sum the currents in the bottom junction we have
- I + I1 + I2 + I3 = 0 (0.32) The only difference between equations 0.25 and 0.26 is that one is the negative of the other. Numerical solution of both equations will give the same answer.
Resistors in Parallel.
Suppose we have three resistors in parallel as in Figure 0.8a and we wish to replace them with a single resistor as in Figure 0.8b. We want a single resistor Req which will cause the same amount of current to flow as the parallel combination of R1, R2 and R3 when connected across the same voltage source (battery). In other words we want one resistor which will act the same as the three resistors together.

Figure 0.8 (a) Three Resistors in Parallel,
(b) One Equivalent Resistor to Replace it.
For a verbal description click here.
We now apply a voltage E to the resistors as shown in Figure 0.9. Kirchhoff's equation for the bottom line of the circuit is -I + I1 + I2 + I3 = 0. Solving for I givesI = I1 + I2 + I3 (0.33) The equivalent resistor Req would give the simple equation
I = Ieq (0.34) If we substitute Ohm's law IN = E / RN and remember that the voltage E is the same everywhere in a parallel circuit we have
E / Req = E / R1 + E / R2 + E / R3 (0.35) canceling E
1 / Req = 1 / R1 + 1 / R2 + 1 / R3 (0.35) in the general form and as more often written
Req = 1 / ( 1 / R1 + 1 / R2 + ... + 1 / RN) (0.37) Equation 0.37 says that the equivalent of any number of resistors in parallel is the reciprocal of the sum of all of the reciprocals of the individual resistors in parallel.

Figure 0.9 (a) Three Paralleled Resistors Connected to a
Voltage Source, (b) One Equivalent Resistor
Connected to a Similar Voltage Source
For a verbal description click here.
Logical Checks.
When finding the equivalent of parallel resistors the equivalent will always be less than the smallest single resistor.Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
0.5 Prefixes.
Prefixes are used throughout the sciences to indicate multiplication by a power of ten. You probably already know that 1 centimeter = 10-2 meters and 1 kilogram = 103 grams.In electricity and magnetism the values are so large or so small as to require the use of prefixes. You MUST be able to make instant conversions in your head from one prefix to another or the unprefixed unit. Here are the prefixes you should know.
For a more screen reader friendly version of the table below click here.
Prefix Multiplier Symbol pico 10-12 p nano 10-9 n micro 10-6 u milli 10-3 m kilo 103 k mega 106 M giga 109 G Table 0.1 List of Prefixes Commonly Used in Electronics
For a more screen reader friendly version of this table click here.
Example 0.2.
Convert; (a) 500,000 hertz to kilohertz and megahertz,
(b) 820 k ohms (kilohms) to ohms and Megohms,
(c) 9 x 10-4 amperes to mA and uA.Solution
(a) 500 kilohertz (kHz) and 0.5 megahertz (MHz)
(b) 820,000 ohms and 0.82 M ohms
(c) 0.9 mA and 900 �AYou should be able to answer those questions as quickly as you can speak the words. If you cannot, make up some practice questions and drill until you can convert without having to stop and think.
Yes, it's memorization. Unfortunately there is no other way to learn prefixes. There is nothing to understand, just memorize, memorize, memorize.
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
0.6 Numerical Examples
The following examples will illustrate the standard method for solving electric circuits. The method employs the repeated application of Ohm's and Kirchhoff's laws. The examples will also illustrate prefix conversion. In solving these circuits there is no formula you can find to plug numbers into. You must think!Example 0.3.
In the circuit of Figure 0.2 the battery voltage E is 24.00 volts. R1 = 470 ohms, R2 = 220 ohms and R3 = 330 ohms. What is the current drawn from the battery?Solution:
The equivalent resistance in the circuit is R1 + R2 + R3 = 470 ohms + 220 ohms + 330 ohms = 1020 ohms. The current drawn from the battery is I = E / Req I = 24 v / 1020 ohms = 2.35 x 10-2 A = 23.5 mA.Example 0.4.
In the circuit of Figure 0.2 the resistance of each resistor is as follows. R1 = 910 ohms, R2 = 1.1 k ohms and R3 = 1.3 k ohms. The voltage across R2 is 4.985 volts. What is the battery voltage?Solution:
Intermediate results should always be carried out to four significant digits. Answers should be rounded off to three significant digits. The current in R2 is I2 = V2 / R2 = 4.985 v / 1.1 k ohms = 4.532 mA. This also is the current in R1 and R3, I = I1 = I2 = I3. The voltage across R1 is V1 = I1 x R1 = 4.532 mA x 910 ohms = 4.124 v, V2 is given and V3 = 5.892 v. The battery voltage E is equal to the sum of all resistor voltages E = 4.124 v + 4.985 v + 5.892 v = 15.001 v. Rounding off, the battery voltage E = 15.0 volts.Example 0.5.
In the circuit of Figure 0.6 the resistance of R2 is 620 ohms and the current through it is 125 mA. The resistance of R3 is 15 k ohms. What is the current through R3?Solution:
The voltage across R2 is V2 = I2 x R2 = 125 mA x 620 ohms = 77.50 v. In a parallel circuit E = V1 = V2 = V3; hence V3 = 77.50 v. I3 = V3 / R3 = 77.50 v / 15 k ohms = 5.17 mA.Example 0.6.
In figure 0.6 the current in R1 is 66.6 mA, the current in R2 is 39.4 mA, the power in R3 is 1.7 watts and the resistance of R3 is 820 ohms. What is the total battery current?Solution:
The current in R3 is I3 = (P / R)1/2 I3 = (1.7 w / 820 ohms)1/2 = 4.553 x 10-2 A = 45.53 mA. The battery current I = I1 + I2 +I3 I = 66.6 mA + 39.4 mA + 45.53 mA = 152 mA.Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
0.7 Capacitance.
A capacitor is a device which has the property of capacitance. Capacitance is the property possessed by a capacitor. Eh?A capacitor is nothing more than an open circuit. Yet it is the most useful open circuit ever discovered. A capacitor consists of two conductors separated by an insulator. Capacitors can best be described as devices which permit electric charge to be stored and released in a controllable and repeatable manner.
Capacitance is that electrical property which resists changes in the voltage across the circuit containing the capacitance.
Capacitors are devices in which energy can be stored for short periods of time. The energy is stored in the electric field between the two conductors of the capacitor.
Capacitance is defined as
C = Q / V (0.38) where C is called the capacitance and is measured in farads, Q is the charge on either conductor in coulombs and V is the potential difference between the two conductors in volts.
If equation 0.38 is solved for charge we have
Q = C V (0.39) If we take the time derivative of both sides of this equation we have
dq / dt = C dv / dt (0.40) But dq/dt = i; therefore,
i = C dv / dt (0.41) This equation turns out to be much more useful than you might imagine.
Example 0.7.
If the current through a capacitor is 120 milliamperes and the rate of change of voltage is to be 1.5 volts/milliseconds, what is the capacitance?Solution:
Solving equation 0.41 for C givesC = I / (dv/dt) = 120 x 10-3 / (1.5 v / 10-3) = 8.0 x 10-5 farads.
8 x 10-5 farads may be expressed as 80 microfarads or 80 uf. Both answers are correct, they are just different ways of expressing the same number.
Equation 0.41 tells us that we cannot change the voltage across a capacitor in zero time. If we tried, the current would be infinite. This equation also tells us that if we maintain a constant current through a capacitor, the voltage across it will change linearly with time. This is the basis of the linear sweep in an oscilloscope.
Resistance-Capacitance Circuit.

Figure 0.10 Circuit For Charging and Discharging a Capacitor.
For a verbal description click here.
Consider the circuit of Figure 0.10. The switch is placed in position 1 to insure that there is no initial charge on the capacitor. Then the switch is changed to position 2 and the capacitor begins to charge. The bottom plate will receive a negative charge while the top plate will receive a positive charge. Kirchhoff's voltage equation for this circuit at any instant of time isE = iR + q / C (0.42) The battery voltage E, the resistance R and the capacitance C do not vary with time. The current i and the charge on the capacitor q do vary with time. If we take the time derivative of this equation we haveE = di / dt x R + dq / dt x 1 / C (0.43) If we make the substitution i = dq/dt we haveE = di / dt x R + i / C (0.44) The solution to this differential equation in i isi = E / R x e-t/RC (0.45) This equation tells us that the current starts out as if the capacitor were a short circuit. i0+ = E/R. The current quickly falls away and decays exponentially.When t becomes equal to RC the value of the exponent on e is -1. This point in time has been defined as the time constant of the circuit and is given as
T = RC (0.46) where T is the time-constant in seconds, R is the resistance in ohms and C is the capacitance in farads.After one time-constant the current has fallen to 1/e of its initial value; after 2 time-constants the current has fallen to e-2 of its initial value and so on. Theoretically the current will never reach zero. After 5 time-constants the current will be .07% of its initial value and for most practical purposes may be considered to be zero.
Example 0.8.
Starting with equation 0.45 and using only Ohm's and Kirchhoff's laws show that the voltage across the capacitor is given byvC = E (1 - e-t/RC) (0.47)
Solution:
The voltage across the resistor is vR = iR orBack to Fun with Transistors.vR = E e-t/RC (0.48)
Solving Kirchhoff's equation for vC gives
vC = E - vR (0.49)
Substituting equation 0.48 into 0.49 and factoring out an E gives us
vC = E (1 - e-t/RC) (0.50)
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
0.8 Inductance.
Inductance is that electrical property which resists changes in the current in the circuit containing the inductance.A device which has the property of inductance is called an inductor. It consists of a coil of wire. The coil may be wound on a solid iron core, a powdered iron core or a hollow tube (air core).
An inductor can store and release energy. The energy is stored in the magnetic field which is produced by the current flowing in the coil of wire.
Inductance is defined as
L = N H / I (0.51) where L is the inductance which is given in units called henrys, N is the number of turns on the coil, H is the magnetic flux produced by each turn and I is the current in the coil.If we rearrange equation 0.51 we have
L I = N H (0.52) If we take the time derivative of equation 0.52 we haveL di / dt = N dH / dt (0.53) Remember from physics thatE = - N dH /dt (0.54) Substituting equation 0.54 into equation 0.53 yieldsE = - L di / dt (0.55) This equation tells us that we cannot change the current through an inductor in zero time. To do so would require an infinite voltage across the inductor.The minus sign in equation 0.55 tells us that the polarity of the voltage which is produced is in such a direction as to oppose the change which produced it.
Consider the circuit of Figure 0.11. The battery will cause current to flow to the right in the inductor (coil of wire). The normal polarity of the voltage drop across the inductor will be positive to the left as shown in the figure.

Figure 0.11 Simple Inductive Circuit.
For a verbal description click here.
If we now cause a sudden decrease in the voltage of the "battery" the current through the inductor will decrease. This is a negative di/dt. Combined with the minus sign in equation 0.55 gives a positive result. The current is flowing to the right in the inductor. A positive voltage with respect to this current means that the voltage will be positive on the right as shown. For the period of time that the change of current is taking place, the inductor may be considered as a voltage generator. The "voltage generator" in the inductor which has its positive terminal on the right is adding to the voltage of the battery. Remember that this whole thing started with a decrease in the battery voltage. The voltage being produced by the inductor is adding to the battery voltage and thereby opposing the change.If we now cause a sudden increase in the voltage of the "battery" the current through the inductor will increase. This is a positive di/dt. Combined with the minus sign in equation 0.55 gives a negative result. The current is flowing to the right in the inductor. A negative voltage with respect to this current means that the voltage will be negative on the right as shown. For the period of time that the change of current is taking place, the inductor may be considered as a voltage generator. The "voltage generator" in the inductor which has its negative terminal on the right is subtracting from the voltage of the battery. Remember that this whole thing started with an increase in the battery voltage. The voltage being produced by the inductor is opposing the change.
The inductor only has a finite amount of energy stored in its magnetic field and it cannot maintain the voltage indefinitely. The inductor cannot prevent the change in current but it can slow it down.
Example 0.9.
A relay coil has an inductance of 95 millihenrys. A transistor switch turns off a current of 40 mA through the coil in a time of 1 us. What is the magnitude of the voltage spike which is produced?Solution:
E = L di / dt = 95 mH x 40 mA / 1 us = 3800 volts.Resistive-Inductive Circuits.
Figure 0.12 is the diagram of an inductive-resistive (RL) circuit. The switch is placed in position 1 to insure that there is no current in the circuit. When the switch is changed to position 2 the battery's potential is applied to the series RL circuit. For an infinitesimal instant of time, no current will flow in the circuit. The inductor has developed an emf of the polarity indicated in the figure. If the voltage across the battery and the inductor have the same magnitude and sign, Kirchhoff's law says that there is no voltage drop across the resistor. If there is no voltage across the resistor, there is no current through it. Because this is a series circuit, no current in the resistor means no current anywhere in the circuit. This situation cannot last for any finite length of time. Current begins to increase in the circuit but the change continues to be opposed by the inductor. The inductor ultimately loses the fight and the current becomes equal to E/R assuming that the inductor has zero resistance (a highly invalid assumption as it turns out).

Figure 0.12 Resistive-Inductive Circuit With Switch.
For a verbal description click here.
Now let us write Kirchhoff's equation for the circuit of Figure 0.12.E = iR + L di / dt (0.56) The solution to this equation isi = E / R (1 - e-tR/L) (0.57) This equation tells us that the current starts out as if the inductor were an open circuit. i0+ = 0. The current quickly rises to exponentially approach E/R.The voltage across the inductor is
vL = E e-tR/L (0.58) Verification of equation 0.58 is left as an exercise for the student.When t becomes equal to L/R the value of the exponent on e is -1. This point in time has been defined as the time constant of the circuit and is given as
T = L/R (0.59) where T is the time-constant in seconds, R is the resistance in ohms and L is the inductance in henrys.After one time-constant the current has risen to 1 - 1/e of its initial value; after 2 time-constants the current has risen to 1 - e-2 of its initial value and so on. Theoretically the current will never reach the maximum value of E/R. After 5 time-constants the current will be 99.83% of E/r and for most practical purposes may be considered to be E/r.
The Reality of Inductors.
In the foregoing, inductance and resistance were treated as if they were separate components of the circuit. In practice, inductors always have resistance. Inductors are coils of wire. Wire has resistance. It is impossible to make an inductor which does not have any resistance.For purposes of circuit analysis the inductance of a coil and its resistance are shown schematically as separate circuit elements. In the circuit of Figure 0.12 it is likely that the resistor and inductor which are shown actually represent a single coil of wire. Think of it as being roughly analogous to the X and Y components of a force.
Recent advances in superconductors may eventually make the preceding paragraphs unnecessary. However, at the present time, it is not possible to form superconducting materials into a wire and wind it into a coil. Note: That's still true in 2007.
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
0.9 Problems.
- Two spheres are charged with +25 and +50 microcoulombs respectively. The distance between them is 20 meters. What is the force exerted between the two spheres? Is the force attractive or repulsive?
- Express the ampere in terms of kilograms, meters and seconds.
- If a current of 500 mA flows for 11 minutes, how much charge is moved?
- If a charge of 1026 coulombs was transferred at a constant rate in a time of 3 hours, what was the current?
- A current of 25 mA must be left on until a charge of 10,000 coulombs has been moved. How long must the current be left on? Express your answer in days, hours, minutes and seconds.
- Express the volt in terms of kilograms, meters and seconds.
- If 300 joules of work are done on 25 coulombs of charge, what was the potential through which the charge was moved?
- If 12 coulombs are moved through a potential of 120 volts, how much work was done?
- If 420 joules of work are done while moving a certain amount of charge through a potential difference of 28 volts, how much charge was moved?
- If 15 amperes are drawn from a 12 volt battery, what is the power?
- What is the current drawn by a 100 watt, 120 volt light bulb?
- For proper operation an electroplating cell requires the movement of 1.26 x 105 coulombs per hour. The cell voltage is 3.3 volts. How much power is required to keep the cell in continuous operation?
- Express the ohm in terms of kilograms, meters and seconds.
- A current of 55 mA is flowing through a 270 ohm resistor. What is the voltage drop across the resistor?
- When a potential of 12 volts is applied to an unknown resistor, a current of 24.74 mA flows. What is the resistance of the resistor?
- If a 56 ohm resistor is placed across a 15 volt power supply, how much current will flow?
- A resistor substitution box contains the following resistor values.
First decade 15, 22, 33, 47, 68 and 100 ohms Second decade 150, 220, 330, 470, 680 and 1000 ohms
Each successive decade follows the same pattern. The highest resistance is 10 Megohms. Each resistor can dissipate a maximum of 1 watt without burning out. (a) What is the minimum resistance setting which can be safely connected across the 120 volt power line?
(b) What is the minimum resistance setting which can be safely connected across a 20 volt power supply?
(c) What is the minimum resistance setting which can be safely connected across a 12 volt power supply?
(d) What is the minimum resistance setting which can be safely connected across a 5 volt power supply?- How much current can safely be run through; (a) a 39 ohm 1/2 watt resistor, (b) a 470 ohm 1/4 W resistor, (c) a 27 ohm 2 W resistor and (d) a 560 ohm 1 W resistor?
- In Figure 0.2, E = 6.60 volts, R1 = 33 ohms, R2 = 22 ohms and R3 = 11 ohms. How much current is flowing in the circuit?
- In Figure 0.2, E = 7.20 volts, R1 = 470 ohms, R2 = 220 ohms and R3 = 100 ohms. What is (a) the voltage across R1, (b) the voltage across R2 and (c) the voltage across R3?
- In Figure 0.2, R1 = 2.2 k ohms, R2 = 1.5 k ohms and R3 = 3.6 k ohms. If the voltage across R1 (V1) is 2.45 volts, what is the voltage across R3 (V3)?
- In Figure 0.2, E = 22.5 volts, R1 = 3.9 k ohms, R3 = 4.7 k ohms, V2 = 7.500 v and V3 = 8.198 v. What is the resistance of R2?
- In Figure 0.6, E = 6.60 volts, R1 = 33 ohms, R2 = 22 ohms and R3 = 11 ohms. How much current is flowing in the circuit?
- In Figure 0.6, the battery current I = 200 mA, R1 = 470 ohms, R2 = 220 ohms and R3 = 100 ohms. What is; (a) the current through R1, (b) the current through R2 and (c) the current through R3?
- In Figure 0.6, R1 = 2.2 k ohms, R2 = 1.5 k ohms and R3 = 3.6 k ohms. If I1 = 8.182 mA, what is I3?
- In Figure 0.6, I = 5.987 mA, R1 = 3.9 k ohms, R3 = 4.7 k ohms, I2 = 1.765 mA, and I3 = 1.915 mA. What is the resistance of R2?
- How much charge is stored on a 7000 uf capacitor when it is charged to a voltage of 18 volts?
- A circuit has a capacitance of 100 pf. How much current must the circuit deliver to the capacitor in order to change the voltage at a rate of 13 v/us?
- If a 2000 uf capacitor is being discharged with a current of 1 A, how much will its voltage change in 8 ms?
- In the circuit of Figure 0.10 if R = 1 Meg ohm, C = 1 uf and E = 10.0 v. The capacitor starts out fully discharged. How long after the switch is thrown to position 2 does the voltage across the capacitor reach 9.0 volts?
- A time delay circuit triggers when the voltage reaches 2/3 of the applied voltage. The capacitor always starts charging from 0 volts. It is desired that the circuit will trigger 1.5 seconds after the timing cycle begins. If the capacitor is a 0.1 uf, what value resistor is required in the circuit?
- Starting with equation 0.57 and using only Ohm's and Kirchhoff's laws show that the voltage across an inductor is given by vL = E e-tR/L.
- The current through a 50 millihenry inductor is to be changed from some value IL to zero in a time of 5 us. What must the value of IL be to give a 20 kv voltage spike?
- What is the time-constant of a coil which has 8 henrys of inductance and 40 ohms of resistance?
- A relay is a device which employs an electromagnet to close one or more sets of switch contacts. The switch contacts can carry a much larger current than is required to energize the electromagnet. The electromagnet is a coil of wire which has inductance and resistance. A given relay is taking too long to close its contacts in a particular application. It has been determined that the delay is not due to mechanical inertia of the moving parts but is due to the time- constant of the RL circuit of the coil. Discuss what may be done to shorten the time required for the relay to close. The relay itself may not be replaced or altered.
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
0.10 Answers to problems.
- 3.125 Newtons repulsive.
- Coulombs = meters x Newtons-1 / seconds.
- 330 coulombs.
- 95 mA.
- 4 d: 15 h: 6 m: 40 s.
- Volts = Newton-1 x seconds
- 12 volts.
- 1440 Joules.
- 15 Coulombs.
- 180 watts.
- 0.833 Amps.
- 115.5 watts.
- ohms = seconds2 / meters
- 14.85 volts.
- 485 ohms.
- 268 mA.
- (a) 15 k ohms, (b) 470 ohms, (c) 150 ohms, (d) 15 ohms.
- (a) 113 mA, (b) 23.1 mA, (c) 272 mA, (d) 42.2 mA.
- 100 mA.
- (a) 4.28 volts, (b) 2.00 volts, (c) 0.911 volts.
- 4.01 volts.
- 4.30 k ohms.
- 1.10 Amps.
- (a) 25.5 mA, (b) 54.5 mA, (c) 120 mA.
- 5.00 mA.
- 5.10 k ohms.
- 0.126 Coulombs.
- 1.30 mA.
- 4.00 volts.
- 2.30 seconds.
- 13.6 Meg ohms.
- Beginning with the equation,
i = E / R (1 - e-tR/L) The voltage across the resistor is obtained by multiplying the current by the resistance. Multiplying the equation by R gives,
VR = E (1 - e-tR/L) By Kirchhoff's law,E = VR + VL OrVL = E - VR Subtracting E from the equation for VRVL = E - E (1 - e-tR/L) Removing the parentheses and carrying out the multiplication gives,VL = E - E + E e-tR/L So,VL = E e-tR/L QED.- 2.00 Amps.
- 0.200 seconds.
- Place a resistor in series with the coil and increase the applied voltage to keep the current the same.
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.