Pg_1     go to page number 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

CHAPTER 10

THE ELASTIC LIMIT OF SPACE



INTRODUCTION


The idea that a force that imparts structure to the material world has been around since antiquity. Some of the earliest references to this idea are found in the Hindu scriptures. These scriptures were originated by the ancient Indus Valley civilization at about 3,000 BC. The concept of the Brahman is described in these scriptures. The Brahman is the basis of the material world, the force that holds all things together, and the hidden power that is latent in all things.


Later references to this concept were developed in ancient Greece at about 500 BC. The Greek philosopher Heraclitus spoke of the concept of the Logos. According to Heraclitus the Logos is the source of all order. This source of order is hidden in a deeper reality. Heraclitus believed that seeing this deeper reality is reserved only for the Gods and for those few humans who can escape conventional modes of understanding.


The concept of the Logos was taken up by Philo, a central figure in Judaism, at about 10 AD. Philo concluded that the Logos was the divine power that mediated the universe. To Philo the Logos was the mind of the universe.


In the 19th century Thomas Young, who discovered the wave nature of light, described an ether. Young's ether is the medium in which light travels and matter rests. This ether fixes the speed of light and sets the elementary constants.


Throughout recorded history the concept of a force that gives form and function to the material world has been described by philosophers, theologians, and scientists.


Pg_2 UP


In 1887 the Michelson Morley experiment failed to detect Young's ether. Since that time the concept of an ether has been abandoned by the scientific community. The abandonment of the concept of an ether has resulted in an atomic information crisis. All atomic and sub-atomic particles are identical to other particles of the same type. For example each elementary particle "knows" how much to weigh, how fast to vibrate, and how fast to spin. Without a force that exchanges information, how do elementary particles "know" what to be?   If elementary particles are not restricted to definite states of being (quantum states) the universe would be without order.


Present quantum theory does not embrace the idea that an external source of information determines the quantum states. Claude E. Shannon developed the science of information in 1948. Shannon showed that information is a measurable commodity. 1 As a commodity, information can only be obtained through a communications channel. Hans Christian Von Baeyter writes, 2
" ..in the last two decades physicists have finally realized what they should have understood long ago - that classical mechanics is almost always chaotic...Indeed, it has been proved quite generally that chaos cannot exist in a quantum mechanical system..."
Astronomers reading spectral lines with the help of telescopes have found that all elementary particles (of like types) in the universe are identical. A long range communications channel or exchange force eliminates chaos (the natural tendency of a system) from quantum systems. This communication channel sets the standard of being for the elementary particles. This standard of being is known as the quantum condition.
"Information is physical."
Ralph Landauer IBM Corp.
A mathematical analysis will now be presented. This analysis develops the concept of the elastic limit of space. Extended analysis in the next chapter has shown that the elastic limit of space determines the magnitude of Planck's constant.


Pg_3 UP


Reflections

[75/300 ohm xformer]
Reflections take place when the impedance, of the medium through which the wave travels, changes. For example, on the rear of many television sets there is a matching transformer. (at right ) This transformer matches the coaxial cable's 75 ohms impedance to the 300 ohm impedance of the television's twin lead antenna wire. This matching transformer prevents the television signal from being reflected at the point at which the two cables, each with a different impedance, connect. All reflections, including the one of yourself in a mirror, result from a change in impedance. The reflection of mass energy at the surface of matter is also due to a drastic change in impedance.


Reflections occur when the impedance of the medium, through which the wave travels, changes. Impedance is expressed in units of ohms. The impedance of a mechanical wave is given by equation #1.


Impedance = (MK)1/2

Equation #1 the impedance of a mechanical system


M = mass

K = The spring constant


The same laws of simple harmonic motion apply to all waves. Transmitters send out electromagnetic signals. These signals are traveling waves of energy. These waves have an impedance associated with them. The electrical impedance in ohms is given by Equation #2.


Impedance = (L/C)1/2

Equation #2 The impedance of an electrical system


L = inductance

C = capacitance


A variation in the ratio of inductance to capacitance results in a change in characteristic impedance. This variation reflects waves.


Pg_4 UP


Mediums convey waves of many different frequencies. For example, a coaxial cable can pass many different channels. The inner and outer conductors of a transmission line form a continuous capacitor. Electromagnetic waves passing through the line will intersect a certain segment of this continuous capacitor. The wavelength of the energy passing through the line determines the length of the segment intersected. A segment of a certain length will have a specific value of capacitance and inductance. The values of inductance and capacitance that determine the impedance of a transmission both vary inversely with the frequency of the wave passing through the line.


Pick the icon to view an example of wave motion. Shows a wave traveling down a coaxial cable



This effect also holds the ratio of capacitance to inductance constant. No reflections take place in this constant impedance environment.


Pg_5 UP


Stray capacitance is a phenomena familiar to electrical engineers. The first radios were limited to low frequency operation because of the high value of stray capacitance inherent to the large vacuum tubes and components of the day.


Pick the icon to view an example of the frequency of a technology.



As components were miniaturized, the stray circuit capacitance was reduced. The reduction of stray circuit capacitance allowed electronic circuits to operate at increasingly higher frequencies. Today's miniature chips compute at frequencies which are higher than the frequency at which circuits, of just a few years ago, could oscillate. Stray capacitance is not a phenomena which is limited to the components of electrical circuits. The universe is capacitively coupled to everything within its bounds. This coupling manifests itself as the minimum capacitance of a point. Electrical capacitance is equivalent to the reciprocal mechanical elasticity. The capacitance of a point expresses the elastic limit of free space.

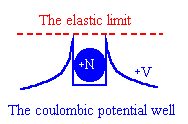
The characteristic impedance of free space is disrupted when the energy density of a field exceeds the ability of space to support the field. At higher energy densities space breaks down like a spring stretched beyond its limit. Matter forms when the intensity of field exceeds the elastic limit of space.


Pg_6 UP


The displacement x in a mechanical system is conceptually equivalent to the reciprocal of the capacitance "1/C" of an electrical system. The electrical charge Q of an electrical system is conceptually equivalent to the spring constant K of a mechanical system. This relationship is exhibited by the following two equations.


force = -K x

voltage = -(q)(1/capacitance)


The spring can be stretched until its material elastic limit is exceeded. The voltage associated with an electrical charge q can increase until space can no longer support the field. This author refers to this breakdown as the elastic limit of space. In an electrical system this breakdown elastic limit can be qualified in reciprocal farads.

This author defines isolated electrical capacitance as the capacitance of a geometric shape that is not under the influence of other charges. The effective geometry of a quantum system was qualified by its isolated electrical capacitance. All of the natural forces experience geometry. They do it in their own unique way. The isolated electrical capacitance of a quantum system expresses a geometry that is experienced by all of the natural forces.

[Graph]


Pg_7 UP


The quantum of capacitance and the rest energy of the electron

The relationship between the energy E and voltage V of a capacitor is given by equation number 1.

E = (1/2) C V2

Substituting the rest energy of the electron for E yields equation 2.

M-ec2 = (1/2) C V2

The relationship between capacitance and charge Q is given by equation number 4.

Q = C V

Substituting equation number 4 into equation number 2 yields equation number 5.

M-ec2 = (1/2) q2/C

Solving for C

C = (1/2) q2 / [M-ec2 ]

Inserting the known value of the rest mass of an election, and setting the electric charge "Q" to one "q" yields the quantum of capacitance Cq. The electromagnetic force experiences the quantum of capacitance through a maximum of intensity. All divergent forces experience a maximum of intensity.


Cq = 1.5677 x 10 -25 Farads

The quantum of capacitance



This equation was placed in a box. This was done to emphasize the importance of the equation.


Pg_8 UP


The quantum of capacitance and the nuclear radius

The strong nuclear force is non-linear. It has attractive and repulsive components. No simple maximum of intensity exists. The nuclear force is very strong. It attempts to crush the nucleons. This crushing effect is limited by the geometry associated with the elastic limit of space. A minimum of displacement is established. All non-divergent forces experience this geometry. The diameter of a proton was qualified with the electromagnetic quantum of capacitance.

The capacitance of a sphere = the quantum of capacitance

4peor = 1.568 x 10-25 Farads

Solving for r yields the maximum radius of the proton. 7 The strengths of electric and strong nuclear forces are equal at this displacement. The equalization of the strength of the forces makes this geometry accessible to both the electromagnetic and the strong nuclear forces.

rp = 1.409 x 10-15 meters

The strong nuclear force experiences the quantum of capacitance through a minimum of displacement.


Pg_9 UP


THE ELASTIC DISCONTINUITY OF THE GRAVITATIONAL FIELD

The negative gravitational potential of the universe is currently bound to the positive energy of the universe. This coupling expresses itself through a conservation of positive energy. This was not always the case. In the early universe the positive energy of the universe was in a state of transition. This transitional state, as other transitional states, was established through an equalization in the strength of the forces. The strength of the gravitational force was equal to the strength of the other forces. This equalization took place when the universe was about the size of an atom. The strength of the gravitational field has diminished with the expansion of the universe. The product of the radius of the universe and the strength of the gravitational field has remained invariant. The strengths of the nuclear and electromagnetic fields have also remained invariant. The positive energy of the present universe was crystallized by a disparity in the strength of the forces. The elastic limit of space crystallized into the fabric of space at the same instant. The gravitational coupling constant ag expresses the ratio of the current strength of the gravitational to the electric force. This force is measured between and electron and a proton.

ag = 2.27 x 1039

The visible universe effectively extends for 13.3 billion light years. A discontinuity exists at this extent. The quantum condition is an affect of this discontinuity. This extent was expressed in meters.

Eu = 1.26 x 1026 meters


Pg_10 UP


A relationship exists between the strength of forces, the radius of the proton, and the extent of the universe. This relationship is expressed below.

ag = Eu / ( 2p)2 rp

The factor of 4p2 appears in this relationship. This author suspects that the constant is an expression of the gravitational permittivity of free space eg. This concept was discussed on Page 11 of Chapter 6.

The gravitational field acting through the geometry of the universe establishes the magnitude of an elastic discontinuity. The gravitational field experiences the elastic limit of space through its weakness. The magnitude of this discontinuity crystallized into the fabric of space as the early universe cooled. It has remained invariant ever since. This author measures the magnitude of the discontinuity in (gravitational)-Farads.

Cq = 4pegru

The magnitude of eg equals eo divided by the product of the gravitational coupling constant and 4p2.

Cq = 4p [eo / (ag * 4p2 ) ] ru

Cq = 1.5677 x 10 -25 Gravitational-Farads


[animation]
Once gravitationally established, the other forces experience the elastic discontinuity through contact with matter. This process establishes the radius of energetic accessibility.


Pg_11 UP


THE DISPLACEMENT OF ENERGETIC ACCESSIBILITY


A maximum of electrical force is exerted between two electrical charges that are compressed to a displacement equal to the classical radius of the electron. This force maximum is:

Force = Q2 / ( 4peo (2*1.409 x 10-15 )2 ) = 29.053 Newtons

As demonstrated in Chapter 7 this is also the force exerted by the energy trying to escape the confine of a single electron.

Force = Dp / Dt = (2E / c) / (2L / c) = E/L

Force = E / ( 2*1.409 x 10-15 ) = 29.053 Newtons

The mechanical elastic constant of the electron (to be developed ) varies inversely with its displacement. The elastic of the electron is expressed below. It exerts a force of 29.053 Newtons at radius 2rp.

K = 29.053 / rx

The weak nuclear force also interacts at radius rp. This interaction will be presented in Chapter 11.

The strength of the forces exerted by the various fields converges at the radius rp. This is the classical radius of energetic accessibility.


Pg_12 UP


THE ELASTIC ENERGY OF THE ELECTRON


The potential energy of an electron is usually expressed in terms of its electric field. This method of expressing the potential energy of a field cannot explain how local fields are attached.

E = -Q / ( 4peo r )

The elastic energy of a spring is expressed below.

Energy = -1/2 Kx2

The constants in the above equations were regrouped to express the energy of the electron in terms of an elastic constant. The elastic energy of the electron is expressed below. The elastic constant method is useful. It reveals the elastic discontinuties at which local fields are attached

Energy = - 1/2 (29.053/rx) (2rp)2

The elastic constant varies inversely with the displacement of an elastic discontinuity. This displacement is measured from the center of mass of the electron. The proton contains one elastic discontinuity rp. The electron contains two elastic discontinuities 2rp. The mass energy of the electron is pinned into the structure of matter at the first discontinuity. The potential energy of the electron is pinned into the structure of matter at the second discontinuity. The factor of two is the reason that the classical radius of the electron is twice that of the proton. The orbiting electron is separately attached to each force field Z of the nucleus. In general the number of discontinuities contained within the electric field of an orbiting atomic charge equals 2Z. The condition is that of the stationary quantum state.

Energy = 1/2 (29.053/Zrx) (2Zrp)2

Two points of interest were tested. The electron is compressed to its classical radius ( rx= 2*1.409 x 10-15 ) its elastic energy equals its mass energy.

The electron is compressed by an amount equal to its the ground state radius of the hydrogen atom. Its elastic constant at the radius equals 29.053 / rh. The energy contained at this displacement equals the ground state potential energy of the hydrogen atom.

This author has expressed the energy of the electron in terms of an elastic displacement. This expression exposed the elastic discontinuity 2rp. The natural forces are pinned into the structure of matter at this discontinuity. This author's method has also exposed the mechanical elastic constant of the electron ( 29.053 / Zr ). This elastic constant couples the elastic energy to the electron at the Compton frequency. This author's elastic constant method has exposed the geometric properties of the stationary quantum state. These geometric properties emerge as a property of the static condition of the universe.


PROPERTY CONVENTIONAL APPROACH ELASTIC CONSTANT APPROACH RESULTS MATCH
FIELD Q/4pe0(1/r2) 29.053/Zx NO
FORCE Q2/4pe0(1/r2) (29.053/Zx)2Zrp YES
ENERGY ZQ2/4pe0( 1/r) 1/2 (29.053/Zx) (2Zrp)2 YES
FREQUENCY NONE COMPTON NO
WAVELENGTH NONE deBroglie (Compton beat note) NO
VELOCITY LUMINAL TRANSITIONAL NA
CLASSICAL YES YES YES
QUANTUM NO YES NO





Pg_13 UP


The quantum of capacitance and the electronic Compton frequency

The quantum of capacitance determines the Compton frequency the electron. The elastic constant of the electron K-e is a fundamental property of the universe. It is classical and linear. It carries the energy of the electron. The frequency of the electron at the radius of the hydrogen atom will be determined from the elastic constant.

K-e = (max_force) / (radius_of_hydorgen) = 29.053 newtons / .529 x 10-10meters = 5.489 x 1011 newton/meter

The Compton frequency of the electron was then determined from the elastic constant of the electron and the mass of the electron.

Frequency = (1/2p) (Kl / mass of the electron)1/2 = (1/2 p) [ 5.489 x 1011 Newton/meter / 9.1 x 10 -31kg ]1/2

Frequency = 1.236 x 10 20 Hertz

The Compton frequency of the electron is a function of its mass,displacment, and elastic constant.


Pg_14 UP


THE ELASTIC LIMIT OF SPACE AND THE GRAVITY OF AN ELECTRON

The general formula of gravitational induction as given by General Relativity and derived in Chapter 6 is given below.

Field = (G/c2r)(dp/dt)

It was shown in Chapter 7 that force that restrains the mass energy produces the gravitational field of matter. Newton's expression for the gravitational field of matter is presented below.

Field = GM/r2

The above two equations were set equal and solved for mass. The result is given below.

M = (r/c2)(dp/dt)

The restraining force exerted by the electron is fixed at 29.05 Newtons. This force couples the gravitational force into the system at twice the radius of energetic accessibility ( 2*1.409 x 10-15 meters). Inserting 29.053 Newtons into the above equation produces the mass of the electron below.

M-e = 9.1 x 10 -31 kg

The gravitational mass of the electron is determined by internal forces. This force is coupled to the other forces at a radius of rp. The mass of the electron is dependent upon the static condition of the universe.


Pg_15 UP


THE ELASTIC LIMIT OF SPACE AND BETA DECAY

The electron is to large to fit inside a neutron. During beta decay an electron and a anti-neutrino are ejected from a neutron. These particles are created from the available energy at the instant of decay. According to this author's model the electron and the anti-neutrino are crushed by forces beyond their their elastic limit while inside the neutron. The force required to crush an electron beyond its elastic limit of 29 Newtons. During beta decay the crushing force is released.

Mass = Energy / c2

Mass = Force * Distance / c2

A force is 29.05 Newtons is applied through the diameter of the neutron [2 (1.409 x 10-15 meters) ].

M-e = (29.053)(2) (1.409 x 10-15 meters) / c2

M-e = 9.1 x 10 -31 kg

The mass of the beta electron is produced by the force exerted at the elastic limit of space.


Pg_16 UP


THE ELASTIC LIMIT OF SPACE AND ALPHA DECAY

Current models of alpha decay describe an electrostatic potential wall around the nucleus. This potential wall has a limited height. The height of the nuclear potential wall as currently described in the texts is given below.

E = 1 / (4 p e0) ( Z2 / r )

For a single proton the height of the coulombic barrier is.

E = 1 / (4 p e0) ( e2 / 1.409 x 10-15 meters)

E = 1.64 x 10 -13 joules

Expressed in electron volts.

E = 1.64 x 10 -14 joules / ( 1.6 x 10-19joules per ev) = 1.02 x 10+6 ev

This author contends that the height of the nuclear potential wall is determined by the elastic limit of space. The elastic limit gives the height in volts.

Volts = q / C

For a single nucleon the electric charge is q and C is the quantum of capacitance.

E = q / 1.568 x 10 -25

E = 1.02 x 10+6 ev

The agreement of the two results demonstrates that the height of the coulombic nuclear potential wall is determined by the elastic limit of space. The analysis my be extended to nucleons of higher atomic number by factoring in the charge and isotropic capacitance of the nucleus.


Pg_17 UP


THE SPIN OF A PARTICLE

It has been shown that a minimum of gravitational capacitance establishes an elastic discontinuity. The strength of the electric and strong nuclear forces converge at the extent of the discontinuity. It will be shown, in the next chapter, that the weak force is also adjoined in this relationship.

The velocity of sound around the discontinuity is set by the strength of the natural forces and the extent of the discontinuity. This velocity emerges as the spin of a particle. This velocity is 1.094 million meters /second. In the next chapter it will be shown that that this velocity in conjunction with the extent of the elastic displacement determine the quantum condition. The quantum condition is a function of the strength of the natural forces and the extent of the visible universe.



THE TECHNOLOGY OF THE ZERO POINT


Conventional science looks to higher energies to find interesting phenomena. Many new phenomena are observed as fixed parameters thaw (become variable) at higher energies. This author has introduced a new parameter, the quantum of capacitance. The quantum of capacitance thaws at low energies. Understanding the affects produced by a changing quantum of capacitance will allow man to control each of the natural forces. This knowledge will produce a revolution in technology.


Pg_18 UP


CONCLUSION


The capacitance of a point is a classical property. It is established through the action of the gravitational field and the bounds of the universe. Its magnitude is 1.568 x 10-25 Farads. This minimum value of capacitance is coupled to the other forces through contact with matter. The divergent forces experience it through a maximum of intensity. The non-divergent forces experience it through a minimum of displacement. This experience pins the force fields into the structure of matter.


Pg_19 UP


NOTES


  1. "A Mathematical Theory of Communication"
    Claude E. Shannon, Bell System Technical Journal #27, July 1948,

  2. Discover, November 1995, Page 109

  3. "Cosmological Antigravity" Lawrence M. Kruss, Scientific American, December 31, 2002, Pg 36
    "The most recent analysis by our group puts the best-fit age of the universe at 13.4 billion years."

  4. "Elementary Antigravity"
    Frank Znidarsic, Vantage Press, 1989
    Pg 50 "13.5 billion light years".

  5. "New Measurements of Ancient Deuterium Boosts the Baryon Density of the Universe"
    Songala and Tytler, Physics Today, August 1996

  6. Hal Puthoff, PHYSICAL REVIEW A, March 1989
    Hal Puthoff, D.C. Cole, PHYSICAL REVIEW E, August 1993.
    Hal Puthoff, OMNI, "Squeezing Energy From a Vacuum" 2/91

  7. Papers on the the radius of the proton. Common radius to .707 of max is 1.2 Fermi meters, extent values 1.04 to 1.45 Fermi meters

    http://www.citebase.org/fulltext?format=application%2Fpdf&identifier=oai%3AarXiv.org%3Aphysics%2F0405118

    http://www.infim.ro/rrp/2005_57_4/17-795-799.pdf



Since May 2004 this page has been called times.






// end of chapter 10 .....................