En esta sección revisaremos algunos ejemplos de cómo aplicar la integral. En situaciones del mundo real, como hemos mencionado, hay ocasiones que nos vemos en la necesidad de encontrar el cambio acumulado, el área bajo la curva o el valor original de una magnitud a partir de una razón de cambio. Por lo que debemos integrar la función que representa la razón de cambio. A continuación te presentamos una tabla con las principales reglas de integración:
Integrales |
 |
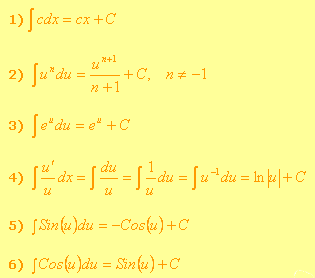Vamos a revisar los siguientes ejemplos:
Ejemplo 1. La ecuación de velocidad de un objeto está dada por 
. Encuentra la ecuación de posición si la posición inicial es x = 5 m.
Solución: En este caso se requiere utilizar la integral para entrar la posición a partir de la razón de cambio. Revisando las reglas de integración podemos utilizar la 1) y 2) para constantes y potencias:
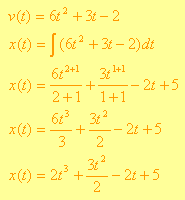
Recuerda que el valor de la posición inicial es que corresponde al valor de C.
Ejemplo 2. Encuentra el área bajo la curva de la función 
entre x = 1 y entre x = 2.
Solución: Para encontrar el área bajo la curva se utiliza la integral definida, es decir la integral y luego se evalúa en los valores establecidos:
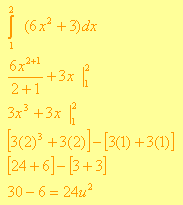
Recuerda que para evaluar debes de sustituir el valor mayor y encontrar el resultado y restarlo al valor menor.
Puedes utilizar los siguientes ejercicios para practicar.
Resuelve los siguientes ejercicios de aplicaciones de derivadas, en todas las situaciones es necesario usar la derivada para encontrar la razón de cambio o la velocidad.
Problema 1. Un vivero suele vender los arbolitos después de 4 años de crecimiento. La razón a la cual crecen en esos 4 años está dada por:
donde t es el tiempo en años y h la altura en centímetros. En el momento de plantarlos, t = 0, miden h = 10 centímetros.
a) Calcula su altura a los t años.
b) ¿Qué altura tienen al momento de venderlos?
Problema 2. Un automóvil parte del reposo y se mueve a lo largo de una carretera recta. Su velocidad en cualquier instante t está dada por la fórmula:
v ( t ) = 3 t 2 mts./seg.
a) Encuentra una fórmula para la posición x ( t ) en función del tiempo t , si su posición inicial es cero.
b) Calcula la distancia recorrida en los primeros 8 segundos.
Problema 3. La velocidad que lleva un automóvil en cualquier instante t está dada por:
En el instante t = 0 el indicador del kilometraje marca 10540 kilómetros.
a) ¿Qué kilometraje marcará a los t segundos?
b) ¿Cuál es el kilometraje a los 100 segundos?
Problema 4. Cuando un cuerpo es lanzado hacia arriba desde el suelo con una velocidad inicial de v 0 = 49 mts./seg. en t = 0, la fórmula para la velocidad a los t seg. es
v ( t ) = 49 – 9.8 t
Calcula la distancia recorrida en el intervalo de tiempo de t = 2 seg. a t = 4 seg.
Problema 5. Calcula el área bajo la curva f ( x ) = x 2 + 1 en el intervalo de x = 1 a x = 3.
Las siguientes ligas te ofrecen otros ejercicios adicionales:
http://www.mundofree.com/fsanchezf/integral.htm
 |
 |
 |
